| NCERT Exemplar Solutions | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 6 Linear Inequalities
Welcome to this essential resource providing comprehensive solutions and detailed explanations for the Class 11 NCERT Exemplar problems focused on Linear Inequalities. This chapter introduces fundamental concepts for handling constraints and relationships that are not strictly equalities, a cornerstone for optimization and decision-making in various fields. The Exemplar questions significantly elevate the challenge beyond standard textbook exercises, demanding a more sophisticated understanding of solving techniques, graphical interpretation, and the ability to model real-world scenarios. Expect problems involving more intricate inequalities, complex systems comprising multiple constraints, inequalities incorporating absolute values, and challenging word problems that require careful formulation before graphical analysis.
Our solutions meticulously cover the methods for solving linear inequalities in one variable. This includes handling inequalities with fractions, brackets, or requiring multiple algebraic steps. We emphasize the critical rule regarding the reversal of the inequality sign when multiplying or dividing both sides by a negative number. Crucially, the solutions demonstrate how to accurately represent the solution set on the number line, paying close attention to the use of open circles (for strict inequalities, $<, >$) and closed circles (for inclusive inequalities, $\le, \ge$) along with appropriate shading. Building upon this, we address solving systems of linear inequalities in one variable, illustrating how to find the final solution set by determining the intersection (common region, often represented using $\cap$) of the individual solution sets on the number line, tackling more complex overlapping or disjoint intervals as presented in the Exemplar.
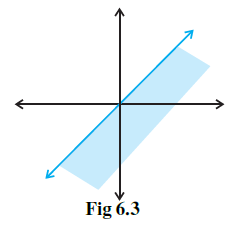
A major focus shifts towards solving linear inequalities in two variables graphically. The solutions provide a clear, step-by-step guide to this visual method:
- Converting the inequality to an equation ($ax+by=c$) to identify the boundary line.
- Determining whether the boundary line should be drawn as a dotted line (for strict inequalities $<, >$) or a solid line (for inclusive inequalities $\le, \ge$).
- Selecting a convenient test point (often $(0,0)$ if it doesn't lie on the line) to determine which half-plane satisfies the inequality.
- Shading the appropriate half-plane that represents the solution set of the inequality.
Furthermore, the solutions tackle problems involving absolute value inequalities, such as $|x-a| < k$ or $|ax+b| \ge c$. We demonstrate algebraic solution techniques, either by considering different cases based on the definition of absolute value or by applying properties like $|X| < k \Leftrightarrow -k < X < k$ and $|X| \ge k \Leftrightarrow X \ge k \text{ or } X \le -k$. The resulting solution sets are often represented on the number line. Finally, significant attention is given to word problems. The solutions guide users through the critical process of translating real-world constraints – involving resource limitations, production requirements, dietary needs, etc. – into a system of linear inequalities. Solving these systems graphically allows for the identification of the feasible set of possibilities, laying crucial groundwork for concepts like Linear Programming encountered later. With clear algebraic steps, precise graphical representations, and logical formulation strategies, this resource is vital for mastering linear inequalities at the Exemplar level.
Solved Examples
Example 1 to 6 (Short Answer Type Questions)
Example 1: Solve the inequality, 3x – 5 < x + 7, when
(i) x is a natural number
(ii) x is a whole number
(iii) x is an integer
(iv) x is a real number
Answer:
Given inequality:
$3x - 5 < x + 7$
Solving the inequality:
Subtract $x$ from both sides:
$3x - 5 - x < x + 7 - x$
$2x - 5 < 7$
Add 5 to both sides:
$2x - 5 + 5 < 7 + 5$
$2x < 12$
Divide by 2:
$\frac{2x}{2} < \frac{12}{2}$
$x < 6$
This is the general solution for the inequality.
(i) When $x$ is a natural number:
The set of natural numbers is $\mathbb{N} = \{1, 2, 3, ...\}$.
We need to find the natural numbers less than 6.
The natural numbers less than 6 are $1, 2, 3, 4, 5$.
The solution set is $\{1, 2, 3, 4, 5\}$.
(ii) When $x$ is a whole number:
The set of whole numbers is $\mathbb{W} = \{0, 1, 2, 3, ...\}$.
We need to find the whole numbers less than 6.
The whole numbers less than 6 are $0, 1, 2, 3, 4, 5$.
The solution set is $\{0, 1, 2, 3, 4, 5\}$.
(iii) When $x$ is an integer:
The set of integers is $\mathbb{Z} = \{..., -3, -2, -1, 0, 1, 2, 3, ...\}$.
We need to find the integers less than 6.
The integers less than 6 are ..., $3, 4, 5$.
The solution set is $\{..., 3, 4, 5\}$.
(iv) When $x$ is a real number:
The set of real numbers is $\mathbb{R}$.
We need to find the real numbers less than 6.
The solution set is the interval $(-\infty, 6)$.
In set-builder notation, the solution set is $\{x \in \mathbb{R} \mid x < 6\}$.
Example 2: Solve $\frac{x - 2}{x + 5}$ > 2
Answer:
Given inequality:
$\frac{x - 2}{x + 5} > 2$
Solving the inequality:
To solve a rational inequality, we first move all terms to one side to compare with 0:
$\frac{x - 2}{x + 5} - 2 > 0$
Find a common denominator:
$\frac{x - 2}{x + 5} - \frac{2(x + 5)}{x + 5} > 0$
Combine the fractions:
$\frac{(x - 2) - 2(x + 5)}{x + 5} > 0$
Simplify the numerator:
$\frac{x - 2 - 2x - 10}{x + 5} > 0$
$\frac{-x - 12}{x + 5} > 0$
Sign Analysis:
The sign of the expression $\frac{-x - 12}{x + 5}$ depends on the signs of the numerator $(-x - 12)$ and the denominator $(x + 5)$. The expression can change sign at the values of $x$ where the numerator or the denominator is zero.
The numerator is zero when $-x - 12 = 0$, which gives $x = -12$.
The denominator is zero when $x + 5 = 0$, which gives $x = -5$. Note that the denominator cannot be zero, so $x \neq -5$.
These values, $-12$ and $-5$, are called critical points. They divide the number line into three intervals:
1. $(-\infty, -12)$
2. $(-12, -5)$
3. $(-5, \infty)$
Now, we test the sign of $\frac{-x - 12}{x + 5}$ in each interval:
Interval $(-\infty, -12)$: Choose a test value, say $x = -13$.
Numerator: $-(-13) - 12 = 13 - 12 = 1$ (Positive)
Denominator: $-13 + 5 = -8$ (Negative)
Fraction: $\frac{\text{Positive}}{\text{Negative}}$ is Negative. Thus, $\frac{-x - 12}{x + 5} > 0$ is false.
Interval $(-12, -5)$: Choose a test value, say $x = -6$.
Numerator: $-(-6) - 12 = 6 - 12 = -6$ (Negative)
Denominator: $-6 + 5 = -1$ (Negative)
Fraction: $\frac{\text{Negative}}{\text{Negative}}$ is Positive. Thus, $\frac{-x - 12}{x + 5} > 0$ is true.
Interval $(-5, \infty)$: Choose a test value, say $x = 0$.
Numerator: $-0 - 12 = -12$ (Negative)
Denominator: $0 + 5 = 5$ (Positive)
Fraction: $\frac{\text{Negative}}{\text{Positive}}$ is Negative. Thus, $\frac{-x - 12}{x + 5} > 0$ is false.
The inequality $\frac{-x - 12}{x + 5} > 0$ is satisfied only in the interval $(-12, -5)$.
We must also ensure that the denominator is not zero, which means $x \neq -5$. The interval $(-12, -5)$ already excludes $-5$.
Solution:
The solution set for the inequality $\frac{x - 2}{x + 5} > 2$ is the interval $(-12, -5)$.
In inequality notation, the solution is $-12 < x < -5$.
Example 3: Solve |3 - 4x| ≥ 9
Answer:
Given inequality:
$|3 - 4x| \ge 9$
Solving the inequality:
The inequality $|A| \ge b$ is equivalent to $A \le -b$ or $A \ge b$.
In this case, $A = 3 - 4x$ and $b = 9$.
So, we need to solve the following two inequalities:
Case 1: $3 - 4x \le -9$
Subtract 3 from both sides:
$3 - 4x - 3 \le -9 - 3$
$-4x \le -12$
Divide by -4 and reverse the inequality sign:
$\frac{-4x}{-4} \ge \frac{-12}{-4}$
$x \ge 3$
Case 2: $3 - 4x \ge 9$
Subtract 3 from both sides:
$3 - 4x - 3 \ge 9 - 3$
$-4x \ge 6$
Divide by -4 and reverse the inequality sign:
$\frac{-4x}{-4} \le \frac{6}{-4}$
$x \le -\frac{6}{4}$
$x \le -\frac{3}{2}$
Combining the solutions:
The solution to $|3 - 4x| \ge 9$ is the union of the solutions from Case 1 and Case 2.
The solution is $x \ge 3$ or $x \le -\frac{3}{2}$.
In interval notation, this is $(-\infty, -\frac{3}{2}] \cup [3, \infty)$.
In set-builder notation, the solution set is $\{x \in \mathbb{R} \mid x \le -\frac{3}{2} \text{ or } x \ge 3\}$.
Example 4: Solve 1 ≤ |x - 2| ≤ 3
Answer:
Given inequality:
$1 \le |x - 2| \le 3$
Breaking down the inequality:
The given double inequality can be separated into two inequalities:
1) $|x - 2| \ge 1$
2) $|x - 2| \le 3$
The solution to the original inequality is the set of $x$ values that satisfy both inequality 1 and inequality 2.
Solving inequality 1: $|x - 2| \ge 1$
The inequality $|A| \ge b$ is equivalent to $A \le -b$ or $A \ge b$.
Applying this rule:
$x - 2 \le -1$ or $x - 2 \ge 1$
Solving the first part:
$x - 2 \le -1$
$x \le -1 + 2$
$x \le 1$
Solving the second part:
$x - 2 \ge 1$
$x \ge 1 + 2$
$x \ge 3$
The solution to $|x - 2| \ge 1$ is $x \le 1$ or $x \ge 3$. In interval notation, this is $(-\infty, 1] \cup [3, \infty)$.
Solving inequality 2: $|x - 2| \le 3$
The inequality $|A| \le b$ is equivalent to $-b \le A \le b$.
Applying this rule:
$-3 \le x - 2 \le 3$
Add 2 to all parts of the inequality:
$-3 + 2 \le x - 2 + 2 \le 3 + 2$
$-1 \le x \le 5$
The solution to $|x - 2| \le 3$ is $-1 \le x \le 5$. In interval notation, this is $[-1, 5]$.
Finding the intersection of the solutions:
We need the values of $x$ that satisfy both $(-\infty, 1] \cup [3, \infty)$ and $[-1, 5]$.
We find the intersection of these two sets:
$((-\infty, 1] \cup [3, \infty)) \cap [-1, 5]$
This intersection is found by considering the parts of the number line where both conditions are met.
The values less than or equal to 1 that are also between -1 and 5 (inclusive) are the values between -1 and 1 (inclusive), i.e., $[-1, 1]$.
The values greater than or equal to 3 that are also between -1 and 5 (inclusive) are the values between 3 and 5 (inclusive), i.e., $[3, 5]$.
The overall solution is the union of these two intervals.
Solution:
The solution set for the inequality $1 \le |x - 2| \le 3$ is $[-1, 1] \cup [3, 5]$.
In inequality notation, the solution is $-1 \le x \le 1$ or $3 \le x \le 5$.
Example 5: The cost and revenue functions of a product are given by
C(x) = 20 x + 4000 and R(x) = 60x + 2000, respectively, where x is the number of items produced and sold. How many items must be sold to realise some profit?
Answer:
Given:
Cost function: $C(x) = 20x + 4000$
Revenue function: $R(x) = 60x + 2000$
Where $x$ is the number of items produced and sold.
To Find:
The number of items ($x$) that must be sold to realise some profit.
Solution:
Profit is defined as Revenue minus Cost.
Let $P(x)$ be the profit function.
$P(x) = R(x) - C(x)$
Substitute the given functions:
$P(x) = (60x + 2000) - (20x + 4000)$
$P(x) = 60x + 2000 - 20x - 4000$
$P(x) = (60x - 20x) + (2000 - 4000)$
$P(x) = 40x - 2000$
To realise some profit, the profit must be greater than zero.
$P(x) > 0$
Substitute the expression for $P(x)$:
$40x - 2000 > 0$
Now, solve the inequality for $x$:
Add 2000 to both sides:
$40x - 2000 + 2000 > 0 + 2000$
$40x > 2000$
Divide by 40 (since 40 is positive, the inequality sign does not change):
$\frac{40x}{40} > \frac{2000}{40}$
$x > 50$
The number of items sold, $x$, must be a whole number since we cannot sell a fraction of an item.
The inequality $x > 50$ means that $x$ must be a whole number strictly greater than 50.
The smallest whole number greater than 50 is 51.
Conclusion:
To realise some profit, more than 50 items must be sold.
Therefore, a minimum of 51 items must be sold.
Example 6: Solve for x, |x + 1| + |x| > 3.
Answer:
Given inequality:
$|x + 1| + |x| > 3$
Solving the inequality using critical points:
The absolute value expressions $|x + 1|$ and $|x|$ change their form depending on the sign of the terms inside.
$|x + 1|$ changes form at $x + 1 = 0$, which is $x = -1$.
$|x|$ changes form at $x = 0$.
These critical points, $x = -1$ and $x = 0$, divide the number line into three intervals:
1. $x < -1$
2. $-1 \le x < 0$
3. $x \ge 0$
Case 1: $x < -1$
In this interval, $x$ is negative and $x+1$ is negative.
So, $|x| = -x$ and $|x + 1| = -(x + 1) = -x - 1$.
The inequality becomes:
$(-x - 1) + (-x) > 3$
$-2x - 1 > 3$
Add 1 to both sides:
$-2x > 4$
Divide by -2 and reverse the inequality sign:
$x < \frac{4}{-2}$
$x < -2$
The solution for this case is $x < -2$. This satisfies the condition $x < -1$.
So, the solution for Case 1 is $(-\infty, -2)$.
Case 2: $-1 \le x < 0$
In this interval, $x$ is negative, but $x+1$ is non-negative.
So, $|x| = -x$ and $|x + 1| = x + 1$.
The inequality becomes:
$(x + 1) + (-x) > 3$
$x + 1 - x > 3$
$1 > 3$
This is a false statement. Therefore, there is no solution in this interval.
Case 3: $x \ge 0$
In this interval, $x$ is non-negative and $x+1$ is non-negative.
So, $|x| = x$ and $|x + 1| = x + 1$.
The inequality becomes:
$(x + 1) + x > 3$
$2x + 1 > 3$
Subtract 1 from both sides:
$2x > 2$
Divide by 2:
$x > \frac{2}{2}$
$x > 1$
The solution for this case is $x > 1$. This satisfies the condition $x \ge 0$.
So, the solution for Case 3 is $(1, \infty)$.
Combining the solutions:
The total solution set is the union of the solutions from all cases.
Solution = (Solution from Case 1) $\cup$ (Solution from Case 2) $\cup$ (Solution from Case 3)
Solution = $(-\infty, -2) \cup \emptyset \cup (1, \infty)$
Solution = $(-\infty, -2) \cup (1, \infty)$
Final Answer:
The solution to the inequality $|x + 1| + |x| > 3$ is $x \in (-\infty, -2) \cup (1, \infty)$.
This can also be written as $x < -2$ or $x > 1$.
Example 7 to 9 (Long Answer Type Questions)
Example 7: Solve for x, $\frac{|x+3|\;+\;x}{x\;+\;2}$ > 1
Answer:
Given inequality:
$\frac{|x+3|\;+\;x}{x\;+\;2} > 1$
Solving the inequality:
First, move all terms to one side:
$\frac{|x+3|\;+\;x}{x\;+\;2} - 1 > 0$
Find a common denominator:
$\frac{|x+3|\;+\;x - (x\;+\;2)}{x\;+\;2} > 0$
Simplify the numerator:
$\frac{|x+3|\;+\;x - x - 2}{x\;+\;2} > 0$
$\frac{|x+3| - 2}{x\;+\;2} > 0$
Identify critical points:
The expression $|x+3|$ changes behavior at $x+3 = 0$, i.e., $x = -3$.
The denominator is zero at $x+2 = 0$, i.e., $x = -2$. The solution must exclude $x = -2$.
These points, $x = -3$ and $x = -2$, divide the number line into three intervals:
1. $x < -3$
2. $-3 \le x < -2$
3. $x > -2$
Case 1: $x < -3$
In this interval, $x+3$ is negative, so $|x+3| = -(x+3) = -x - 3$.
The inequality $\frac{|x+3| - 2}{x\;+\;2} > 0$ becomes:
$\frac{(-x - 3) - 2}{x\;+\;2} > 0$
$\frac{-x - 5}{x\;+\;2} > 0$
To solve $\frac{-x - 5}{x\;+\;2} > 0$, we analyze the signs of the numerator and the denominator. The critical points are $x = -5$ (where numerator is 0) and $x = -2$ (where denominator is 0).
We are in the interval $x < -3$. The relevant critical points are $-5$ and $-2$. These divide the interval $x < -3$ further.
Consider sub-intervals within $x < -3$: $(-\infty, -5)$ and $(-5, -3)$. Note that $x=-2$ is outside $x<-3$, so we only consider $-5$ as a new boundary within this case.
Subcase 1a: $x < -5$
Example value: $x = -6$. Numerator: $-(-6) - 5 = 6 - 5 = 1$ (Positive). Denominator: $-6 + 2 = -4$ (Negative). Fraction: $\frac{\text{Positive}}{\text{Negative}}$ is Negative. $\frac{-x - 5}{x\;+\;2} > 0$ is False.
Subcase 1b: $-5 < x < -3$
Example value: $x = -4$. Numerator: $-(-4) - 5 = 4 - 5 = -1$ (Negative). Denominator: $-4 + 2 = -2$ (Negative). Fraction: $\frac{\text{Negative}}{\text{Negative}}$ is Positive. $\frac{-x - 5}{x\;+\;2} > 0$ is True.
Note that $x=-5$ makes the numerator 0, so the fraction is 0, not greater than 0. So $x=-5$ is excluded.
The solution for $\frac{-x - 5}{x\;+\;2} > 0$ within $x < -3$ is $-5 < x < -3$.
Intersection of $x < -3$ and $-5 < x < -3$ is $-5 < x < -3$.
Solution for Case 1 is $(-5, -3)$.
Case 2: $-3 \le x < -2$
In this interval, $x+3$ is non-negative, so $|x+3| = x+3$.
The inequality $\frac{|x+3| - 2}{x\;+\;2} > 0$ becomes:
$\frac{(x + 3) - 2}{x\;+\;2} > 0$
$\frac{x + 1}{x\;+\;2} > 0$
To solve $\frac{x + 1}{x\;+\;2} > 0$, we analyze the signs of the numerator and the denominator. The critical points are $x = -1$ (where numerator is 0) and $x = -2$ (where denominator is 0).
We are in the interval $-3 \le x < -2$. The relevant critical points are $-2$ and $-1$. These divide the interval $-3 \le x < -2$ further. However, $-1$ is outside the interval $-3 \le x < -2$. So we only consider $-2$ as a boundary within this case.
Subcase 2a: $-3 \le x < -2$
Example value: $x = -2.5$. Numerator: $-2.5 + 1 = -1.5$ (Negative). Denominator: $-2.5 + 2 = -0.5$ (Negative). Fraction: $\frac{\text{Negative}}{\text{Negative}}$ is Positive. $\frac{x + 1}{x\;+\;2} > 0$ is True.
Note that $x=-3$ makes the numerator $|-3+3|-2 = 0-2 = -2$. Denominator is $-3+2 = -1$. $\frac{-2}{-1} = 2 > 0$. So $x=-3$ is included.
The solution for $\frac{x + 1}{x\;+\;2} > 0$ within $-3 \le x < -2$ is $-3 \le x < -2$.
Intersection of $-3 \le x < -2$ and $-3 \le x < -2$ is $-3 \le x < -2$.
Solution for Case 2 is $[-3, -2)$.
Case 3: $x > -2$
In this interval, $x+3$ is non-negative (since $-2 > -3$), so $|x+3| = x+3$.
The inequality $\frac{|x+3| - 2}{x\;+\;2} > 0$ becomes:
$\frac{(x + 3) - 2}{x\;+\;2} > 0$
$\frac{x + 1}{x\;+\;2} > 0$ (Same inequality as in Case 2)
To solve $\frac{x + 1}{x\;+\;2} > 0$, the critical points are $x = -2$ and $x = -1$. We are in the interval $x > -2$. The relevant critical point within this interval is $-1$. This divides the interval $x > -2$ into $(-2, -1)$ and $(-1, \infty)$. Note that $x=-2$ is excluded.
Subcase 3a: $-2 < x < -1$
Example value: $x = -1.5$. Numerator: $-1.5 + 1 = -0.5$ (Negative). Denominator: $-1.5 + 2 = 0.5$ (Positive). Fraction: $\frac{\text{Negative}}{\text{Positive}}$ is Negative. $\frac{x + 1}{x\;+\;2} > 0$ is False.
Subcase 3b: $x > -1$
Example value: $x = 0$. Numerator: $0 + 1 = 1$ (Positive). Denominator: $0 + 2 = 2$ (Positive). Fraction: $\frac{\text{Positive}}{\text{Positive}}$ is Positive. $\frac{x + 1}{x\;+\;2} > 0$ is True.
Note that $x=-1$ makes the numerator 0, so the fraction is 0, not greater than 0. So $x=-1$ is excluded.
The solution for $\frac{x + 1}{x\;+\;2} > 0$ within $x > -2$ is $x > -1$.
Intersection of $x > -2$ and $x > -1$ is $x > -1$.
Solution for Case 3 is $(-1, \infty)$.
Combining the solutions:
The total solution set is the union of the solutions from all cases.
Solution = (Solution from Case 1) $\cup$ (Solution from Case 2) $\cup$ (Solution from Case 3)
Solution = $(-5, -3) \cup [-3, -2) \cup (-1, \infty)$
The union of $(-5, -3)$ and $[-3, -2)$ is $(-5, -2)$.
So, the solution is $(-5, -2) \cup (-1, \infty)$.
Final Answer:
The solution set for the inequality $\frac{|x+3|\;+\;x}{x\;+\;2} > 1$ is $(-5, -2) \cup (-1, \infty)$.
This can also be written as $-5 < x < -2$ or $x > -1$.
Example 8: Solve the following system of inequalities
$\frac{x}{2x \;+\; 1}$ ≥ $\frac{1}{4}$ , $\frac{6x}{4x \;-\; 1}$ < $\frac{1}{2}$
Answer:
Given System of Inequalities:
1) $\frac{x}{2x \;+\; 1}$ ≥ $\frac{1}{4}$
2) $\frac{6x}{4x \;-\; 1}$ < $\frac{1}{2}$
Solving Inequality 1:
$\frac{x}{2x \;+\; 1}$ ≥ $\frac{1}{4}$
Move all terms to one side:
$\frac{x}{2x \;+\; 1} - \frac{1}{4}$ ≥ 0
Find a common denominator:
$\frac{4x - 1(2x \;+\; 1)}{4(2x \;+\; 1)}$ ≥ 0
Simplify the numerator:
$\frac{4x - 2x - 1}{4(2x \;+\; 1)}$ ≥ 0
$\frac{2x - 1}{4(2x \;+\; 1)}$ ≥ 0
Since 4 is a positive constant, the inequality is equivalent to:
$\frac{2x - 1}{2x \;+\; 1}$ ≥ 0
The critical points are where the numerator or denominator is zero:
$2x - 1 = 0 \implies x = \frac{1}{2}$
$2x + 1 = 0 \implies x = -\frac{1}{2}$ (The denominator cannot be zero, so $x \neq -\frac{1}{2}$)
We analyze the sign of the expression $\frac{2x - 1}{2x \;+\; 1}$ in the intervals determined by the critical points $-\frac{1}{2}$ and $\frac{1}{2}$.
- For $x < -\frac{1}{2}$ (e.g., $x = -1$): $\frac{2(-1) - 1}{2(-1) + 1} = \frac{-3}{-1} = 3 > 0$. True.
- For $-\frac{1}{2} < x < \frac{1}{2}$ (e.g., $x = 0$): $\frac{2(0) - 1}{2(0) + 1} = \frac{-1}{1} = -1 < 0$. False.
- For $x > \frac{1}{2}$ (e.g., $x = 1$): $\frac{2(1) - 1}{2(1) + 1} = \frac{1}{3} > 0$. True.
The inequality $\ge 0$ is satisfied when $\frac{2x - 1}{2x \;+\; 1}$ is positive or zero. It is zero at $x = \frac{1}{2}$.
The solution for Inequality 1 is $x < -\frac{1}{2}$ or $x \ge \frac{1}{2}$.
In interval notation: $(-\infty, -\frac{1}{2}) \cup [\frac{1}{2}, \infty)$.
Solving Inequality 2:
$\frac{6x}{4x \;-\; 1}$ < $\frac{1}{2}$
Move all terms to one side:
$\frac{6x}{4x \;-\; 1} - \frac{1}{2}$ < 0
Find a common denominator:
$\frac{2(6x) - 1(4x \;-\; 1)}{2(4x \;-\; 1)}$ < 0
Simplify the numerator:
$\frac{12x - 4x + 1}{2(4x \;-\; 1)}$ < 0
$\frac{8x + 1}{2(4x \;-\; 1)}$ < 0
Since 2 is a positive constant, the inequality is equivalent to:
$\frac{8x + 1}{4x \;-\; 1}$ < 0
The critical points are where the numerator or denominator is zero:
$8x + 1 = 0 \implies x = -\frac{1}{8}$
$4x - 1 = 0 \implies x = \frac{1}{4}$ (The denominator cannot be zero, so $x \neq \frac{1}{4}$)
We analyze the sign of the expression $\frac{8x + 1}{4x \;-\; 1}$ in the intervals determined by the critical points $-\frac{1}{8}$ and $\frac{1}{4}$.
- For $x < -\frac{1}{8}$ (e.g., $x = -1$): $\frac{8(-1) + 1}{4(-1) - 1} = \frac{-7}{-5} = \frac{7}{5} > 0$. False.
- For $-\frac{1}{8} < x < \frac{1}{4}$ (e.g., $x = 0$): $\frac{8(0) + 1}{4(0) - 1} = \frac{1}{-1} = -1 < 0$. True.
- For $x > \frac{1}{4}$ (e.g., $x = 1$): $\frac{8(1) + 1}{4(1) - 1} = \frac{9}{3} = 3 > 0$. False.
The inequality $< 0$ is satisfied when $\frac{8x + 1}{4x \;-\; 1}$ is negative. It is zero at $x = -\frac{1}{8}$, which is not included in $< 0$.
The solution for Inequality 2 is $-\frac{1}{8} < x < \frac{1}{4}$.
In interval notation: $(-\frac{1}{8}, \frac{1}{4})$.
Finding the Intersection:
We need to find the values of $x$ that satisfy both Inequality 1 and Inequality 2.
Solution for Inequality 1: $(-\infty, -\frac{1}{2}) \cup [\frac{1}{2}, \infty)$
Solution for Inequality 2: $(-\frac{1}{8}, \frac{1}{4})$
We need to find the intersection of these two sets:
$( (-\infty, -\frac{1}{2}) \cup [\frac{1}{2}, \infty) ) \cap (-\frac{1}{8}, \frac{1}{4})$
Let's compare the intervals. The critical points are $-\frac{1}{2} = -0.5$, $-\frac{1}{8} = -0.125$, $\frac{1}{4} = 0.25$, and $\frac{1}{2} = 0.5$.
The first solution includes numbers less than $-0.5$ OR greater than or equal to $0.5$.
The second solution includes numbers strictly between $-0.125$ and $0.25$.
Let's check if the interval $(-\frac{1}{8}, \frac{1}{4})$ overlaps with $(-\infty, -\frac{1}{2})$. Since $-\frac{1}{8} = -0.125 > -0.5 = -\frac{1}{2}$, the interval $(-\frac{1}{8}, \frac{1}{4})$ is entirely to the right of $(-\infty, -\frac{1}{2})$. There is no overlap.
Let's check if the interval $(-\frac{1}{8}, \frac{1}{4})$ overlaps with $[\frac{1}{2}, \infty)$. Since $\frac{1}{4} = 0.25 < 0.5 = \frac{1}{2}$, the interval $(-\frac{1}{8}, \frac{1}{4})$ is entirely to the left of $[\frac{1}{2}, \infty)$. There is no overlap.
Since there is no overlap between the solution sets of the two inequalities, their intersection is the empty set.
Final Answer:
The solution set for the given system of inequalities is the empty set, denoted by $\emptyset$ or \{\}.
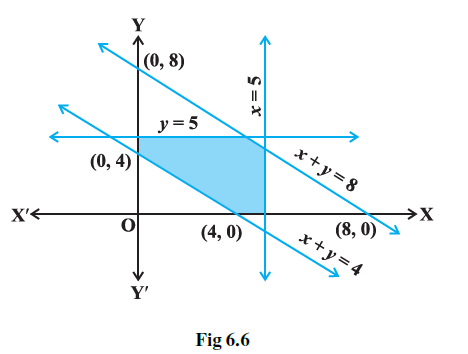
Example 9: Find the linear inequalities for which the shaded region in the given figure is the solution set.

Answer:
Understanding the Problem:
The shaded region represents the feasible region of a system of linear inequalities. The boundaries of the shaded region are lines, and each line corresponds to a linear equation. The inequality is determined by which side of the line the shaded region lies.
Identifying the Boundary Lines:
(Assuming the figure shows a bounded region in the first quadrant, typical for such problems in NCERT Exemplar, bounded by the axes and other lines)
Observing the figure, we can identify the following boundary lines:
1. The y-axis.
2. The x-axis.
3. A vertical line.
4. A horizontal line.
5. A slanted line.
Finding the Equations of the Lines and Corresponding Inequalities:
(Based on common figures in this context, let's assume the lines and points are as follows. The actual analysis would depend on the specific image content.)
1. The y-axis: The equation of the y-axis is $x = 0$. Since the shaded region is in the first quadrant (to the right of the y-axis), the inequality is $x \ge 0$. (Assuming a solid line).
2. The x-axis: The equation of the x-axis is $y = 0$. Since the shaded region is in the first quadrant (above the x-axis), the inequality is $y \ge 0$. (Assuming a solid line).
3. A vertical line: Let's assume this line passes through the point $(4, 0)$ on the x-axis and is vertical. Its equation is $x = 4$. Assuming the shaded region is to the left of this line, the inequality is $x \le 4$. (Assuming a solid line).
4. A horizontal line: Let's assume this line passes through the point $(0, 4)$ on the y-axis and is horizontal. Its equation is $y = 4$. Assuming the shaded region is below this line, the inequality is $y \le 4$. (Assuming a solid line).
5. A slanted line: Let's assume this line passes through the points $(6, 0)$ on the x-axis and $(0, 6)$ on the y-axis. The equation of the line passing through $(a, 0)$ and $(0, b)$ is $\frac{x}{a} + \frac{y}{b} = 1$. So, for $(6, 0)$ and $(0, 6)$, the equation is $\frac{x}{6} + \frac{y}{6} = 1$, which simplifies to $x + y = 6$. To determine the inequality, we can test a point in the shaded region, for example, the origin $(0, 0)$. Substituting $(0, 0)$ into $x+y$: $0 + 0 = 0$. Since the origin is in the shaded region, and $0 < 6$, the inequality is $x + y \le 6$. (Assuming a solid line).
System of Linear Inequalities:
Combining the inequalities from each boundary line, the system of linear inequalities for which the shaded region is the solution set is:
$x \ge 0$
$y \ge 0$
$x \le 4$
$y \le 4$
$x + y \le 6$
Example 10 to 13 (Multiple Choice Questions)
Choose the correct answer from the given four options against each of the Examples 10 to 13 (M.C.Q.)
Example 10: If $\frac{|x - 2|}{x - 2}$ ≥ 0, then
(A) x ∈ [2, ∞)
(B) x ∈ (2, ∞)
(C) x ∈ (– ∞, 2)
(D) x ∈ (– ∞, 2]
Answer:
Given inequality:
$\frac{|x - 2|}{x - 2} \ge 0$
Analysis:
The expression $\frac{|x - 2|}{x - 2}$ is defined only when the denominator is non-zero, i.e., $x - 2 \neq 0$, which means $x \neq 2$.
We consider the definition of the absolute value function:
$|x - 2| = x - 2$ if $x - 2 \ge 0$ (i.e., $x \ge 2$)
$|x - 2| = -(x - 2)$ if $x - 2 < 0$ (i.e., $x < 2$)
Case 1: $x > 2$
In this case, $x - 2 > 0$. So, $|x - 2| = x - 2$.
The inequality becomes:
$\frac{x - 2}{x - 2} \ge 0$
$1 \ge 0$
This is a true statement. So, all values of $x$ such that $x > 2$ are solutions.
This corresponds to the interval $(2, \infty)$.
Case 2: $x < 2$
In this case, $x - 2 < 0$. So, $|x - 2| = -(x - 2)$.
The inequality becomes:
$\frac{-(x - 2)}{x - 2} \ge 0$
$-1 \ge 0$
This is a false statement. So, no values of $x$ such that $x < 2$ are solutions.
Case 3: $x = 2$
As noted earlier, the denominator $x - 2$ is zero when $x = 2$, so the expression is undefined. Thus, $x = 2$ is not a solution.
Combining the results:
The inequality $\frac{|x - 2|}{x - 2} \ge 0$ is true only for $x > 2$.
The solution set is $(2, \infty)$.
Comparing with options:
(A) x ∈ [2, ∞) - Incorrect, includes 2.
(B) x ∈ (2, ∞) - Correct.
(C) x ∈ (– ∞, 2) - Incorrect.
(D) x ∈ (– ∞, 2] - Incorrect, includes 2.
The correct option is (B).
Example 11: The length of a rectangle is three times the breadth. If the minimum perimeter of the rectangle is 160 cm, then
(A) breadth > 20 cm
(B) length < 20 cm
(C) breadth x ≥ 20 cm
(D) length ≤ 20 cm
Answer:
Given:
Length of rectangle $l = 3 \times$ Breadth of rectangle $b$
Minimum perimeter $P_{min} = 160$ cm
To Find:
The inequality relating to the breadth or length.
Solution:
Let the breadth of the rectangle be $b$ cm.
According to the problem, the length of the rectangle is $l = 3b$ cm.
The perimeter of a rectangle is given by the formula $P = 2(l + b)$.
Substitute $l = 3b$ into the perimeter formula:
$P = 2(3b + b)$
$P = 2(4b)$
$P = 8b$
We are given that the minimum perimeter is 160 cm. This means the actual perimeter must be greater than or equal to 160 cm.
$P \ge 160$
Substitute the expression for $P$ in terms of $b$:
$8b \ge 160$
Divide both sides by 8:
$\frac{8b}{8} \ge \frac{160}{8}$
$b \ge 20$
So, the breadth of the rectangle must be greater than or equal to 20 cm.
Matching with options:
Let's examine the given options based on $b \ge 20$:
(A) breadth > 20 cm ($b > 20$)
(B) length < 20 cm ($3b < 20 \implies b < \frac{20}{3}$)
(C) breadth x ≥ 20 cm (Interpreted as breadth $\ge 20$ cm, i.e., $b \ge 20$)
(D) length ≤ 20 cm ($3b \le 20 \implies b \le \frac{20}{3}$)
Option (C) matches our derived inequality $b \ge 20$ cm, assuming 'x' in the option is a typo and it refers to the breadth 'b'.
The correct option is (C).
Example 12: Solutions of the inequalities comprising a system in variable x are represented on number lines as given below, then

(A) x ∈ (– ∞, – 4] ∪ [3, ∞)
(B) x ∈ [– 3, 1]
(C) x ∈ (– ∞, – 4) ∪ [3, ∞)
(D) x ∈ [– 4, 3]
Answer:
Interpretation of the figure:
The figure shows two number lines. Each number line represents the solution set of one inequality in the system.
Identifying individual solution sets from the number lines:
Assuming the standard representation where a shaded region indicates the solution and filled circles indicate inclusion of the endpoint:
From the first number line, the shaded region appears to be the interval from -3 to 1, including both endpoints. Let this solution set be $S_1$.
$S_1 = [-3, 1]$
From the second number line, the shaded region appears to be the interval from -4 to 3, including both endpoints. Let this solution set be $S_2$.
$S_2 = [-4, 3]$
Finding the solution to the system:
The solution to a system of inequalities is the intersection of the solution sets of the individual inequalities.
The solution set for the system is $S_1 \cap S_2$.
$S_1 \cap S_2 = [-3, 1] \cap [-4, 3]$
To find the intersection of two intervals $[a, b]$ and $[c, d]$, the result is $[\max(a, c), \min(b, d)]$, provided $\max(a, c) \le \min(b, d)$.
Here, $a = -3$, $b = 1$, $c = -4$, $d = 3$.
$\max(-3, -4) = -3$
$\min(1, 3) = 1$
Since $\max(-3, -4) = -3 \le 1 = \min(1, 3)$, the intersection is $[-3, 1]$.
Comparing with options:
The solution set is $[-3, 1]$.
Let's compare this with the given options:
(A) x ∈ $(-\infty, -4] \cup [3, \infty)$
(B) x ∈ $[-3, 1]$
(C) x ∈ $(-\infty, -4) \cup [3, \infty)$
(D) x ∈ $[-4, 3]$
The derived solution set $[-3, 1]$ matches option (B).
Example 13: If |x + 3| ≥ 10 , then
(A) x ∈ (– 13, 7]
(B) x ∈ (– 13, 7]
(C) x ∈ (– ∞, – 13] ∪ [7, ∞)
(D) x ∈ [– ∞, – 13] ∪ [7, ∞)
Answer:
Given inequality:
$|x + 3| \ge 10$
Solving the inequality:
The inequality of the form $|A| \ge b$ is equivalent to $A \le -b$ or $A \ge b$.
In this case, $A = x + 3$ and $b = 10$.
We solve the two resulting inequalities:
Case 1: $x + 3 \le -10$
Subtract 3 from both sides:
$x + 3 - 3 \le -10 - 3$
$x \le -13$
Case 2: $x + 3 \ge 10$
Subtract 3 from both sides:
$x + 3 - 3 \ge 10 - 3$
$x \ge 7$
Combining the solutions:
The solution to the original inequality is the union of the solutions from Case 1 and Case 2.
The solution is $x \le -13$ or $x \ge 7$.
In interval notation, $x \le -13$ is represented as $(-\infty, -13]$.
In interval notation, $x \ge 7$ is represented as $[7, \infty)$.
The combined solution set is $(-\infty, -13] \cup [7, \infty)$.
Comparing with options:
Let's compare our solution with the given options:
(A) x ∈ (– 13, 7]
(B) x ∈ (– 13, 7]
(C) x ∈ (– ∞, – 13] ∪ [7, ∞)
(D) x ∈ [– ∞, – 13] ∪ [7, ∞)
Option (C) exactly matches our derived solution set.
Note that option (D) uses incorrect notation for the interval $(-\infty, ...]$.
The correct option is (C).
Example 14 (True or False)
Example 14: State whether the following statements are True or False.
(i) If x > y and b < 0, then bx < by
(ii) If xy > 0, then x > 0, and y < 0
(iii) If xy < 0, then x > 0, and y > 0
(iv) If x > 5 and x > 2, then x ∈ (5, ∞)
(v) If |x | < 5, then x ∈ (– 5, 5)
(vi) Graph of x > – 2 is
(vii) Solution set of x – y ≤ 0 is
Answer:
Let's evaluate each statement:
(i) If $x > y$ and $b < 0$, then $bx < by$
When an inequality is multiplied by a negative number, the direction of the inequality sign is reversed. Given $x > y$ and $b < 0$, multiplying both sides by $b$ gives $x \times b < y \times b$, which is $bx < by$.
True
(ii) If $xy > 0$, then $x > 0$, and $y < 0$
If the product of two numbers is positive ($xy > 0$), it means that both numbers must have the same sign. Either both $x$ and $y$ are positive ($x > 0$ and $y > 0$) or both are negative ($x < 0$ and $y < 0$). The statement claims that $x > 0$ and $y < 0$, which would result in $xy < 0$.
False
(iii) If $xy < 0$, then $x > 0$, and $y > 0$
If the product of two numbers is negative ($xy < 0$), it means that the numbers must have opposite signs. Either $x > 0$ and $y < 0$ or $x < 0$ and $y > 0$. The statement claims that $x > 0$ and $y > 0$, which would result in $xy > 0$.
False
(iv) If $x > 5$ and $x > 2$, then $x \in (5, \infty)$
The condition "x > 5 and x > 2" requires $x$ to satisfy both inequalities simultaneously. Any number greater than 5 is also greater than 2. Therefore, the intersection of the solution sets $x > 5$ and $x > 2$ is simply $x > 5$. The interval notation for $x > 5$ is $(5, \infty)$.
True
(v) If $|x | < 5$, then $x \in (– 5, 5)$
The inequality $|x| < k$ (for $k > 0$) is equivalent to $-k < x < k$. In this case, $k=5$, so $|x| < 5$ is equivalent to $-5 < x < 5$. The interval notation for $-5 < x < 5$ is $(-5, 5)$.
True
(vi) Graph of $x > – 2$ is ... (image)
The inequality $x > -2$ represents all points $(x, y)$ in the plane where the x-coordinate is greater than -2. Graphically, this is the region to the right of the vertical line $x = -2$. Since the inequality is strict ($>$), the boundary line $x = -2$ should be drawn as a dashed line. Assuming the accompanying image correctly depicts a dashed vertical line at $x = -2$ with the region to its right shaded, the statement is true.
True (Assuming the image is the correct graph)
(vii) Solution set of $x – y \le 0$ is ... (image)
The inequality $x - y \le 0$ can be rewritten as $x \le y$ or $y \ge x$. The boundary line is $x - y = 0$, or $y = x$. Since the inequality includes equality ($\le$), the boundary line $y = x$ should be drawn as a solid line. To find the shaded region, we can test a point not on the line, say $(1, 0)$. Substituting into $x - y \le 0$, we get $1 - 0 \le 0 \implies 1 \le 0$, which is false. So the shaded region is on the opposite side of the line from $(1, 0)$. Testing $(0, 1)$: $0 - 1 \le 0 \implies -1 \le 0$, which is true. So the region above the line $y = x$ is shaded. Assuming the accompanying image correctly depicts a solid line $y=x$ with the region above it shaded, the statement is true.
True (Assuming the image is the correct graph)
Example 15 (Fill in the Blanks)
Example 15: Fill in the blanks in the following:
(i) If x ≥ – 3, then x + 5 ................... 2
(ii) If – x ≤ – 4, then 2x ................... 8
(iii) If $\frac{1}{x - 2}$ < 0, then x ………..2
(iv) If a < b and c < 0, then $\frac{a}{c}$ …… $\frac{b}{c}$
(v) If |x - 1| ≤ 2 , then - 1 …… x………..3
(vi) If |3x - 7| > 2, then x …… $\frac{5}{3}$ or x ….. 3
(vii) If p > 0 and q < 0, then p + q ... p
Answer:
(i) If $x \ge – 3$, then $x + 5 \ldots 2$
Given $x \ge -3$. Adding 5 to both sides, we get $x + 5 \ge -3 + 5$, which simplifies to $x + 5 \ge 2$.
Fill in the blank with $\ge$.
(ii) If – $x \le – 4$, then $2x \ldots 8$
Given $-x \le -4$. Multiplying both sides by -1 and reversing the inequality sign, we get $x \ge 4$. Now, multiplying both sides by 2, we get $2x \ge 8$.
Fill in the blank with $\ge$.
(iii) If $\frac{1}{x - 2} < 0$, then $x \ldots 2$
For the fraction $\frac{1}{x - 2}$ to be negative, the numerator and the denominator must have opposite signs. The numerator is 1, which is positive. Therefore, the denominator $x - 2$ must be negative.
$x - 2 < 0$
Adding 2 to both sides gives $x < 2$.
Fill in the blank with $<$.
(iv) If $a < b$ and $c < 0$, then $\frac{a}{c} \ldots \frac{b}{c}$
When an inequality is divided by a negative number, the direction of the inequality sign is reversed. Given $a < b$ and $c < 0$, dividing by $c$ gives $\frac{a}{c} > \frac{b}{c}$.
Fill in the blank with $>$.
(v) If $|x - 1| \le 2$, then $- 1 \ldots x \ldots 3$
The inequality $|x - 1| \le 2$ is equivalent to $-2 \le x - 1 \le 2$. Adding 1 to all parts of the inequality, we get $-2 + 1 \le x - 1 + 1 \le 2 + 1$, which simplifies to $-1 \le x \le 3$.
Fill in the blanks with $\le$ and $\le$.
(vi) If $|3x - 7| > 2$, then $x \ldots \frac{5}{3}$ or $x \ldots 3$
The inequality $|3x - 7| > 2$ is equivalent to $3x - 7 < -2$ or $3x - 7 > 2$.
Solving $3x - 7 < -2$: $3x < -2 + 7 \implies 3x < 5 \implies x < \frac{5}{3}$.
Solving $3x - 7 > 2$: $3x > 2 + 7 \implies 3x > 9 \implies x > 3$.
The solution is $x < \frac{5}{3}$ or $x > 3$.
Fill in the blanks with $<$ and $>$.
(vii) If $p > 0$ and $q < 0$, then $p + q \ldots p$
We are comparing $p+q$ and $p$. Consider the difference $(p + q) - p = q$. Since $q < 0$, the difference is negative, meaning $p + q < p$.
Fill in the blank with $<$.
Exercise
Question 1 to 12 (Short Answer Type Questions)
Solve for x, the inequalities in Exercises 1 to 12
Question 1. $\frac{4}{x + 1}$ ≤ 3 ≤ $\frac{6}{x + 1}$ , (x > 0)
Answer:
Given inequality:
$\frac{4}{x + 1} \le 3 \le \frac{6}{x + 1}$
Given condition: $x > 0$
The compound inequality can be split into two separate inequalities:
1) $\frac{4}{x + 1} \le 3$
2) $3 \le \frac{6}{x + 1}$
Solving Inequality 1:
$\frac{4}{x + 1} \le 3$
Move all terms to one side:
$\frac{4}{x + 1} - 3 \le 0$
Find a common denominator:
$\frac{4 - 3(x + 1)}{x + 1} \le 0$
Simplify the numerator:
$\frac{4 - 3x - 3}{x + 1} \le 0$
$\frac{1 - 3x}{x + 1} \le 0$
We need to find the values of $x$ for which this expression is less than or equal to 0. The critical points are where the numerator or denominator is zero:
$1 - 3x = 0 \implies 3x = 1 \implies x = \frac{1}{3}$
$x + 1 = 0 \implies x = -1$
The expression can change sign at $x = -1$ and $x = \frac{1}{3}$. These points divide the number line into three intervals: $(-\infty, -1)$, $(-1, \frac{1}{3}]$, and $[\frac{1}{3}, \infty)$. Note that $x = -1$ is excluded because the denominator cannot be zero.
However, we are given the condition $x > 0$. So we only need to consider the intersection of $x > 0$ with the solution of $\frac{1 - 3x}{x + 1} \le 0$.
Since $x > 0$, the denominator $x + 1$ is always positive ($x + 1 > 1$).
For $\frac{1 - 3x}{x + 1} \le 0$ to be true when $x + 1 > 0$, the numerator $(1 - 3x)$ must be less than or equal to zero.
$1 - 3x \le 0$
$1 \le 3x$
$\frac{1}{3} \le x$
So, the solution to Inequality 1 under the condition $x > 0$ is $x \ge \frac{1}{3}$.
Solving Inequality 2:
$3 \le \frac{6}{x + 1}$
Move all terms to one side:
$0 \le \frac{6}{x + 1} - 3$
$\frac{6}{x + 1} - 3 \ge 0$
Find a common denominator:
$\frac{6 - 3(x + 1)}{x + 1} \ge 0$
Simplify the numerator:
$\frac{6 - 3x - 3}{x + 1} \ge 0$
$\frac{3 - 3x}{x + 1} \ge 0$
Factor the numerator:
$\frac{3(1 - x)}{x + 1} \ge 0$
Since 3 is a positive constant, the inequality is equivalent to:
$\frac{1 - x}{x + 1} \ge 0$
We need to find the values of $x$ for which this expression is greater than or equal to 0. The critical points are where the numerator or denominator is zero:
$1 - x = 0 \implies x = 1$
$x + 1 = 0 \implies x = -1$ (The denominator cannot be zero, so $x \neq -1$)
The expression can change sign at $x = -1$ and $x = 1$. These points divide the number line into three intervals: $(-\infty, -1)$, $(-1, 1]$, and $[1, \infty)$. Note that $x = -1$ is excluded.
We are given the condition $x > 0$. So we only need to consider the intersection of $x > 0$ with the solution of $\frac{1 - x}{x + 1} \ge 0$.
Since $x > 0$, the denominator $x + 1$ is always positive ($x + 1 > 1$).
For $\frac{1 - x}{x + 1} \ge 0$ to be true when $x + 1 > 0$, the numerator $(1 - x)$ must be greater than or equal to zero.
$1 - x \ge 0$
$1 \ge x$
$x \le 1$
So, the solution to Inequality 2 under the condition $x > 0$ is $0 < x \le 1$.
Combining the solutions:
The solution to the original system of inequalities is the intersection of the solutions from Inequality 1 (under $x > 0$) and Inequality 2 (under $x > 0$), combined with the initial condition $x > 0$.
Solution for Inequality 1 under $x > 0$: $x \ge \frac{1}{3}$
Solution for Inequality 2 under $x > 0$: $0 < x \le 1$
We need to find the intersection of the interval $[\frac{1}{3}, \infty)$ and the interval $(0, 1]$.
The intersection of $x \ge \frac{1}{3}$ and $x \le 1$ is $\frac{1}{3} \le x \le 1$.
The condition $x > 0$ is already satisfied since $\frac{1}{3} > 0$.
The solution is $\frac{1}{3} \le x \le 1$.
In interval notation, the solution is $[\frac{1}{3}, 1]$.
Question 2. $\frac{|x \;-\; 2|\;-\;1}{|x \;-\; 2|\;-\;2}$ ≤ 0
Answer:
Given inequality:
$\frac{|x \;-\; 2|\;-\;1}{|x \;-\; 2|\;-\;2} \le 0$
Solving the inequality:
Let $y = |x - 2|$. Since absolute value is always non-negative, we know $y \ge 0$.
The inequality becomes:
$\frac{y - 1}{y - 2} \le 0$
Also, the denominator cannot be zero, so $|x - 2| - 2 \neq 0$, which means $|x - 2| \neq 2$, or $y \neq 2$.
We need the expression $\frac{y - 1}{y - 2}$ to be non-positive. This occurs when the numerator and denominator have opposite signs, or when the numerator is zero.
Case A: Numerator $\ge 0$ and Denominator $< 0$
$y - 1 \ge 0 \implies y \ge 1$
$y - 2 < 0 \implies y < 2$
Combining these, we get $1 \le y < 2$.
Case B: Numerator $\le 0$ and Denominator $> 0$ (This case gives no solution since if the numerator is $\le 0$ and denominator $>0$, the fraction is $\le 0$ only if numerator is 0, but we covered numerator=0 in Case A's $\ge 0$ condition).
Let's use the critical point method for $\frac{y - 1}{y - 2} \le 0$ with $y \ge 0$ and $y \neq 2$.
Critical points for $y$ are $y=1$ and $y=2$. Consider intervals for $y$ on the number line, keeping in mind $y \ge 0$.
Interval 1: $0 \le y < 1$. Test $y=0.5$. $\frac{0.5 - 1}{0.5 - 2} = \frac{-0.5}{-1.5} = \frac{1}{3}$. $\frac{1}{3} \le 0$ is False.
Interval 2: $1 \le y < 2$. Test $y=1.5$. $\frac{1.5 - 1}{1.5 - 2} = \frac{0.5}{-0.5} = -1$. $-1 \le 0$ is True. Also $y=1$ gives $\frac{0}{-1} = 0 \le 0$, True. So $1 \le y < 2$ is part of the solution.
Interval 3: $y > 2$. Test $y=3$. $\frac{3 - 1}{3 - 2} = \frac{2}{1} = 2$. $2 \le 0$ is False.
The solution for $y$ is $1 \le y < 2$.
Substituting back for $x$:
We have $1 \le |x - 2| < 2$.
This is a compound inequality which means we must satisfy both $1 \le |x - 2|$ and $|x - 2| < 2$.
First inequality: $|x - 2| \ge 1$.
This means $x - 2 \le -1$ or $x - 2 \ge 1$.
$x - 2 \le -1 \implies x \le 1$.
$x - 2 \ge 1 \implies x \ge 3$.
The solution for $|x - 2| \ge 1$ is $x \in (-\infty, 1] \cup [3, \infty)$.
Second inequality: $|x - 2| < 2$.
This means $-2 < x - 2 < 2$.
Add 2 to all parts:
$-2 + 2 < x - 2 + 2 < 2 + 2$
$0 < x < 4$.
The solution for $|x - 2| < 2$ is $x \in (0, 4)$.
Finding the intersection:
The solution to the original inequality is the intersection of the solutions to the two parts:
$((-\infty, 1] \cup [3, \infty)) \cap (0, 4)$
Intersection of $(-\infty, 1]$ and $(0, 4)$ is $(0, 1]$.
Intersection of $[3, \infty)$ and $(0, 4)$ is $[3, 4)$.
The union of these two intervals is the final solution.
Solution set:
The solution set is $(0, 1] \cup [3, 4)$.
Question 3. $\frac{1}{|x|\;-\;3}$ ≤ $\frac{1}{2}$
Answer:
Given inequality:
$\frac{1}{|x| - 3} \le \frac{1}{2}$
Note that the expression is defined only if $|x| - 3 \neq 0$, which means $|x| \neq 3$. This implies $x \neq 3$ and $x \neq -3$.
Solving the inequality:
Let $y = |x|$. Since $|x| \ge 0$, we have $y \ge 0$. The inequality becomes:
$\frac{1}{y - 3} \le \frac{1}{2}$
where $y \ge 0$ and $y \neq 3$.
Move all terms to one side:
$\frac{1}{y - 3} - \frac{1}{2} \le 0$
Find a common denominator:
$\frac{2 \cdot 1 - 1 \cdot (y - 3)}{2(y - 3)} \le 0$
Simplify the numerator:
$\frac{2 - y + 3}{2(y - 3)} \le 0$
$\frac{5 - y}{2(y - 3)} \le 0$
Since 2 is a positive constant, the inequality is equivalent to:
$\frac{5 - y}{y - 3} \le 0$
Sign analysis for y:
We need the expression $\frac{5 - y}{y - 3}$ to be less than or equal to zero. The critical points are where the numerator or denominator is zero: $y = 5$ and $y = 3$. Remember $y \neq 3$ and $y \ge 0$. We consider intervals for $y$ while respecting $y \ge 0$ and $y \neq 3$.
- For $0 \le y < 3$: (e.g., $y=0$) $\frac{5-0}{0-3} = \frac{5}{-3} < 0$. True.
- For $3 < y \le 5$: (e.g., $y=4$) $\frac{5-4}{4-3} = \frac{1}{1} = 1 > 0$. False. At $y=5$, $\frac{0}{2} = 0 \le 0$. True. So $y=5$ is included.
- For $y > 5$: (e.g., $y=6$) $\frac{5-6}{6-3} = \frac{-1}{3} < 0$. True.
The solution for $y$ is $0 \le y < 3$ or $y \ge 5$.
Substituting back $y = |x|$:
We have the conditions:
1) $0 \le |x| < 3$
2) $|x| \ge 5$
Solving $0 \le |x| < 3$:
Since $|x| \ge 0$ is always true for any real $x$, we only need to consider $|x| < 3$.
$|x| < 3 \implies -3 < x < 3$.
The solution set for this part is $(-3, 3)$.
Solving $|x| \ge 5$:
$|x| \ge 5 \implies x \le -5$ or $x \ge 5$.
The solution set for this part is $(-\infty, -5] \cup [5, \infty)$.
Combining the solution sets:
The solution to the original inequality is the union of the solutions from the two parts.
Solution set = $(-3, 3) \cup ((-\infty, -5] \cup [5, \infty))$
Rearranging the intervals in order:
Final Answer:
The solution set is $(-\infty, -5] \cup (-3, 3) \cup [5, \infty)$.
Question 4. |x - 1| ≤ 5, |x| ≥ 2
Answer:
Given system of inequalities:
1) $|x - 1| \le 5$
2) $|x| \ge 2$
Solving Inequality 1:
$|x - 1| \le 5$
This inequality is of the form $|A| \le b$, which is equivalent to $-b \le A \le b$.
So, we have:
$-5 \le x - 1 \le 5$
Add 1 to all parts of the inequality:
$-5 + 1 \le x - 1 + 1 \le 5 + 1$
$-4 \le x \le 6$
The solution set for the first inequality is the interval $[-4, 6]$.
Solving Inequality 2:
$|x| \ge 2$
This inequality is of the form $|A| \ge b$, which is equivalent to $A \le -b$ or $A \ge b$.
So, we have:
$x \le -2$ or $x \ge 2$
The solution set for the second inequality is $(-\infty, -2] \cup [2, \infty)$.
Finding the intersection:
The solution to the system of inequalities is the intersection of the solution sets of the individual inequalities.
We need to find the intersection of $[-4, 6]$ and $(-\infty, -2] \cup [2, \infty)$.
This can be found by taking the intersection of $[-4, 6]$ with each part of the second set and then taking the union of the results.
$[-4, 6] \cap (-\infty, -2]$: The numbers that are $\ge -4$ and $\le 6$ AND $\le -2$. This results in $[-4, -2]$.
$[-4, 6] \cap [2, \infty)$: The numbers that are $\ge -4$ and $\le 6$ AND $\ge 2$. This results in $[2, 6]$.
The intersection of the two original solution sets is the union of these resulting intervals.
Solution set:
The solution set for the system of inequalities is $[-4, -2] \cup [2, 6]$.
In inequality notation, the solution is $-4 \le x \le -2$ or $2 \le x \le 6$.
Question 5. - 5 ≤ $\frac{2 - 3x}{4}$ ≤ 9
Answer:
Given inequality:
$-5 \le \frac{2 - 3x}{4} \le 9$
Solving the inequality:
The given compound inequality can be separated into two individual inequalities that must both be satisfied:
1) $-5 \le \frac{2 - 3x}{4}$
2) $\frac{2 - 3x}{4} \le 9$
Solving Inequality 1:
$-5 \le \frac{2 - 3x}{4}$
Multiply all parts of the inequality by 4 (since 4 is positive, the inequality direction does not change):
$4 \times (-5) \le 4 \times \left(\frac{2 - 3x}{4}\right)$
$-20 \le 2 - 3x$
Subtract 2 from both sides:
$-20 - 2 \le 2 - 3x - 2$
$-22 \le -3x$
Divide both sides by -3. Remember to reverse the inequality sign when dividing by a negative number:
$\frac{-22}{-3} \ge \frac{-3x}{-3}$
$\frac{22}{3} \ge x$
This can also be written as $x \le \frac{22}{3}$.
Solving Inequality 2:
$\frac{2 - 3x}{4} \le 9$
Multiply both sides of the inequality by 4 (since 4 is positive, the inequality direction does not change):
$4 \times \left(\frac{2 - 3x}{4}\right) \le 4 \times 9$
$2 - 3x \le 36$
Subtract 2 from both sides:
$2 - 3x - 2 \le 36 - 2$
$-3x \le 34$
Divide both sides by -3. Remember to reverse the inequality sign when dividing by a negative number:
$\frac{-3x}{-3} \ge \frac{34}{-3}$
$x \ge -\frac{34}{3}$
Combining the solutions:
The solution to the original compound inequality is the set of all $x$ values that satisfy both $x \le \frac{22}{3}$ and $x \ge -\frac{34}{3}$.
Combining these two inequalities, we get:
$-\frac{34}{3} \le x \le \frac{22}{3}$
In interval notation, the solution is $[-\frac{34}{3}, \frac{22}{3}]$.
Final Answer:
The solution set for the inequality $-5 \le \frac{2 - 3x}{4} \le 9$ is $[-\frac{34}{3}, \frac{22}{3}]$.
Question 6. 4x + 3 ≥ 2x + 17 , 3x - 5 < -2.
Answer:
Given system of inequalities:
1) $4x + 3 \ge 2x + 17$
2) $3x - 5 < -2$
Solving Inequality 1:
$4x + 3 \ge 2x + 17$
Subtract $2x$ from both sides:
$4x + 3 - 2x \ge 2x + 17 - 2x$
$2x + 3 \ge 17$
Subtract 3 from both sides:
$2x + 3 - 3 \ge 17 - 3$
$2x \ge 14$
Divide both sides by 2:
$\frac{2x}{2} \ge \frac{14}{2}$
$x \ge 7$
The solution set for the first inequality is $[7, \infty)$.
Solving Inequality 2:
$3x - 5 < -2$
Add 5 to both sides:
$3x - 5 + 5 < -2 + 5$
$3x < 3$
Divide both sides by 3:
$\frac{3x}{3} < \frac{3}{3}$
$x < 1$
The solution set for the second inequality is $(-\infty, 1)$.
Finding the intersection:
The solution to the system of inequalities is the intersection of the solution sets of the individual inequalities.
We need to find the intersection of $[7, \infty)$ and $(-\infty, 1)$.
The interval $[7, \infty)$ includes all numbers greater than or equal to 7.
The interval $(-\infty, 1)$ includes all numbers strictly less than 1.
There is no number that is both greater than or equal to 7 and strictly less than 1.
The intersection of these two intervals is empty.
Solution set:
The solution set for the given system of inequalities is the empty set, denoted by $\emptyset$ or \{\}.
Question 7. A company manufactures cassettes. Its cost and revenue functions are C(x) = 26,000 + 30x and R(x) = 43x, respectively, where x is the number of cassettes produced and sold in a week. How many cassettes must be sold by the company to realise some profit?
Answer:
Given:
Cost function: $C(x) = 26000 + 30x$
Revenue function: $R(x) = 43x$
Where $x$ is the number of cassettes produced and sold in a week.
To Find:
The number of cassettes ($x$) that must be sold to realise some profit.
Solution:
Profit $P(x)$ is calculated as the difference between Revenue and Cost.
$P(x) = R(x) - C(x)$
Substitute the given functions:
$P(x) = (43x) - (26000 + 30x)$
$P(x) = 43x - 26000 - 30x$
$P(x) = (43x - 30x) - 26000$
$P(x) = 13x - 26000$
To realise some profit, the profit must be strictly greater than zero.
$P(x) > 0$
Substitute the expression for $P(x)$:
$13x - 26000 > 0$
Now, solve the inequality for $x$:
Add 26000 to both sides:
$13x - 26000 + 26000 > 0 + 26000$
$13x > 26000$
Divide both sides by 13 (since 13 is positive, the inequality sign does not change):
$\frac{13x}{13} > \frac{26000}{13}$
$x > 2000$
Since $x$ represents the number of cassettes sold, it must be a whole number (a non-negative integer). The inequality $x > 2000$ means that $x$ must be a whole number strictly greater than 2000.
The smallest whole number greater than 2000 is 2001.
Conclusion:
To realise some profit, the company must sell more than 2000 cassettes.
Therefore, the minimum number of cassettes to be sold is 2001.
Question 8. The water acidity in a pool is considerd normal when the average pH reading of three daily measurements is between 8.2 and 8.5. If the first two pH readings are 8.48 and 8.35, find the range of pH value for the third reading that will result in the acidity level being normal.
Answer:
Given:
First pH reading ($r_1$) = 8.48
Second pH reading ($r_2$) = 8.35
Let the third pH reading be $r_3$.
The average pH reading of the three measurements is $\frac{r_1 + r_2 + r_3}{3}$.
The normal range for the average pH is between 8.2 and 8.5 (exclusive, as per the term "between").
Condition for normal acidity:
$8.2 < \text{Average pH} < 8.5$
$8.2 < \frac{8.48 + 8.35 + r_3}{3} < 8.5$
Solving the inequality for $r_3$:
First, sum the known readings:
$8.48 + 8.35 = 16.83$
The inequality becomes:
$8.2 < \frac{16.83 + r_3}{3} < 8.5$
Multiply all parts of the inequality by 3:
$3 \times 8.2 < 3 \times \left(\frac{16.83 + r_3}{3}\right) < 3 \times 8.5$
$24.6 < 16.83 + r_3 < 25.5$
Subtract 16.83 from all parts of the inequality:
$24.6 - 16.83 < 16.83 + r_3 - 16.83 < 25.5 - 16.83$
$7.77 < r_3 < 8.67$
Conclusion:
For the water acidity to be normal, the third pH reading must be strictly between 7.77 and 8.67.
The range of pH values for the third reading is $(7.77, 8.67)$.
Question 9. A solution of 9% acid is to be diluted by adding 3% acid solution to it. The resulting mixture is to be more than 5% but less than 7% acid. If there is 460 litres of the 9% solution, how many litres of 3% solution will have to be added?
Answer:
Given:
Volume of 9% acid solution = 460 litres.
Concentration of the first solution = 9% = 0.09.
Concentration of the second solution to be added = 3% = 0.03.
The resulting mixture concentration must be between 5% and 7% (exclusive).
Required concentration range: 5% < Concentration < 7%, which is $0.05 < \text{Concentration} < 0.07$.
To Find:
The number of litres of 3% solution that must be added.
Solution:
Let $x$ be the number of litres of 3% acid solution added ($x \ge 0$).
The amount of acid in the 9% solution is $0.09 \times 460$ litres.
$0.09 \times 460 = 41.4$ litres.
The amount of acid in $x$ litres of 3% solution is $0.03 \times x$ litres.
The total volume of the mixture is $460 + x$ litres.
The total amount of acid in the mixture is $41.4 + 0.03x$ litres.
The concentration of acid in the resulting mixture is $\frac{\text{Total amount of acid}}{\text{Total volume}} = \frac{41.4 + 0.03x}{460 + x}$.
According to the problem, the concentration must be between 0.05 and 0.07:
$0.05 < \frac{41.4 + 0.03x}{460 + x} < 0.07$
Since $x$ represents volume, $x \ge 0$, so $460 + x > 0$. We can multiply all parts of the inequality by $(460 + x)$ without changing the inequality direction.
$0.05(460 + x) < 41.4 + 0.03x < 0.07(460 + x)$
Split this into two inequalities:
Inequality 1: $0.05(460 + x) < 41.4 + 0.03x$
Inequality 2: $41.4 + 0.03x < 0.07(460 + x)$
Solving Inequality 1:
$0.05(460) + 0.05x < 41.4 + 0.03x$
$23 + 0.05x < 41.4 + 0.03x$
$0.05x - 0.03x < 41.4 - 23$
$0.02x < 18.4$
$x < \frac{18.4}{0.02}$
$x < \frac{1840}{2}$
$x < 920$
Solving Inequality 2:
$41.4 + 0.03x < 0.07(460) + 0.07x$
$41.4 + 0.03x < 32.2 + 0.07x$
$41.4 - 32.2 < 0.07x - 0.03x$
$9.2 < 0.04x$
$x > \frac{9.2}{0.04}$
$x > \frac{920}{4}$
$x > 230$
Combining the results:
We have the conditions $x < 920$ and $x > 230$. Combining these, we get $230 < x < 920$.
We also know that $x \ge 0$ (volume cannot be negative). The interval $(230, 920)$ satisfies $x \ge 0$.
Conclusion:
The number of litres of 3% solution that must be added should be more than 230 litres and less than 920 litres.
The range of the number of litres of 3% solution to be added is $(230, 920)$.
Question 10. A solution is to be kept between 40°C and 45°C. What is the range of temperature in degree fahrenheit, if the conversion formula is F = $\frac{9}{5}$ C + 32?
Answer:
Given:
The temperature range in Celsius is between 40°C and 45°C. This can be written as an inequality:
$40 < C < 45$
The conversion formula from Celsius (C) to Fahrenheit (F) is:
$F = \frac{9}{5} C + 32$
To Find:
The range of temperature in degree Fahrenheit.
Solution:
We need to find the corresponding range for F when $40 < C < 45$. We will use the given conversion formula to transform the inequality.
Start with the inequality for C:
$40 < C < 45$
First, multiply all parts of the inequality by $\frac{9}{5}$. Since $\frac{9}{5}$ is a positive number, the direction of the inequality signs does not change.
$\frac{9}{5} \times 40 < \frac{9}{5} C < \frac{9}{5} \times 45$
Simplify the multiplication:
$\frac{9 \times 40}{5} < \frac{9}{5} C < \frac{9 \times 45}{5}$
$9 \times 8 < \frac{9}{5} C < 9 \times 9$
$72 < \frac{9}{5} C < 81$
Next, add 32 to all parts of the inequality. This operation does not change the direction of the inequality signs.
$72 + 32 < \frac{9}{5} C + 32 < 81 + 32$
Perform the addition:
$104 < \frac{9}{5} C + 32 < 113$
Now substitute $F = \frac{9}{5} C + 32$ into the inequality:
$104 < F < 113$
Conclusion:
The range of temperature in degree Fahrenheit is between 104°F and 113°F.
In interval notation, the range is $(104, 113)$.
Question 11. The longest side of a triangle is twice the shortest side and the third side is 2cm longer than the shortest side. If the perimeter of the triangle is more than 166 cm then find the minimum length of the shortest side.
Answer:
Given:
Let the shortest side of the triangle be $s$ cm.
The longest side is twice the shortest side, so its length is $2s$ cm.
The third side is 2 cm longer than the shortest side, so its length is $s + 2$ cm.
The perimeter of the triangle is more than 166 cm.
To Find:
The minimum length of the shortest side ($s$).
Solution:
The perimeter of a triangle is the sum of the lengths of its three sides.
Perimeter $= (\text{shortest side}) + (\text{longest side}) + (\text{third side})$
Perimeter $= s + 2s + (s + 2)$
Perimeter $= (s + 2s + s) + 2$
Perimeter $= 4s + 2$
According to the problem, the perimeter is more than 166 cm. This can be written as an inequality:
$4s + 2 > 166$
Now, we solve this linear inequality for $s$.
Subtract 2 from both sides of the inequality:
$4s + 2 - 2 > 166 - 2$
$4s > 164$
Divide both sides by 4. Since 4 is a positive number, the direction of the inequality sign does not change.
$\frac{4s}{4} > \frac{164}{4}$
$s > 41$
This inequality tells us that the length of the shortest side, $s$, must be strictly greater than 41 cm.
We should also consider the triangle inequality theorem, which states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side. Since $s$ must be a length, $s > 0$. The lengths of the sides are $s$, $2s$, and $s+2$. For these to form a triangle, we need:
$s + 2s > s + 2 \implies 3s > s + 2 \implies 2s > 2 \implies s > 1$
$s + (s + 2) > 2s \implies 2s + 2 > 2s \implies 2 > 0$ (This is always true)
$2s + (s + 2) > s \implies 3s + 2 > s \implies 2s > -2 \implies s > -1$
Combining $s > 41$ with the triangle inequality conditions ($s > 1$, $2 > 0$, $s > -1$) and $s > 0$, the most restrictive condition is $s > 41$.
So, the length of the shortest side $s$ must be a real number strictly greater than 41 cm.
The set of all possible values for the shortest side is the open interval $(41, \infty)$.
In this context, "minimum length" refers to the lower bound of the possible values for $s$. Since the inequality is strict ($s > 41$), the value 41 is not included in the set of possible lengths, and there is no single minimum value in the set $(41, \infty)$. However, the shortest side must be strictly greater than 41 cm to satisfy the given condition about the perimeter.
Conclusion:
The shortest side must have a length greater than 41 cm.
Thus, the minimum length of the shortest side is more than 41 cm.
If the question implies that the length must be an integer, the minimum integer length would be 42 cm.
Question 12. In drilling world’s deepest hole it was found that the temperature T in degree celcius, x km below the earth’s surface was given by T = 30 + 25 (x – 3), 3 ≤ x ≤ 15. At what depth will the temperature be between 155°C and 205°C?
Answer:
Given:
Temperature formula: $T = 30 + 25(x - 3)$, where $T$ is the temperature in degrees Celsius and $x$ is the depth in km.
Valid range for depth: $3 \le x \le 15$ km.
Required temperature range: $155^\circ\text{C} < T < 205^\circ\text{C}$.
To Find:
The range of depth $x$ for which the temperature $T$ is between $155^\circ\text{C}$ and $205^\circ\text{C}$.
Solution:
We are given the temperature range $155 < T < 205$.
Substitute the formula for $T$ into this inequality:
$155 < 30 + 25(x - 3) < 205$
This is a compound inequality. We solve it for $x$ by applying operations to all three parts simultaneously.
Subtract 30 from all parts:
$155 - 30 < 30 + 25(x - 3) - 30 < 205 - 30$
$125 < 25(x - 3) < 175$
Divide all parts by 25. Since 25 is a positive number, the direction of the inequalities does not change.
$\frac{125}{25} < \frac{25(x - 3)}{25} < \frac{175}{25}$
$5 < x - 3 < 7$
Add 3 to all parts:
$5 + 3 < x - 3 + 3 < 7 + 3$
$8 < x < 10$
This inequality $8 < x < 10$ gives the range of depths where the temperature is between $155^\circ\text{C}$ and $205^\circ\text{C}$.
Considering the given depth constraint:
The formula for the temperature is given for the range $3 \le x \le 15$.
We need to find the values of $x$ that satisfy both the condition $8 < x < 10$ and the condition $3 \le x \le 15$.
The intersection of the interval $(8, 10)$ and the interval $[3, 15]$ is the set of numbers that are strictly greater than 8 and strictly less than 10, AND are also greater than or equal to 3 and less than or equal to 15.
Since $8 < x < 10$ implies $x$ is between 8 and 10, any number in this range is automatically within the range $[3, 15]$ (since $3 \le 8$ and $10 \le 15$).
Therefore, the intersection is simply the interval $(8, 10)$.
Conclusion:
The temperature will be between $155^\circ\text{C}$ and $205^\circ\text{C}$ at a depth between 8 km and 10 km.
The range of depth is $(8, 10)$ km.
Question 13 to 18 (Long Answer Type Questions)
Question 13. Solve the following system of inequalities $\frac{2x + 1}{7x - 1}$ > 5, $\frac{x + 7}{x - 8}$ > 2
Answer:
Given system of inequalities:
1) $\frac{2x + 1}{7x - 1} > 5$
2) $\frac{x + 7}{x - 8} > 2$
Solving Inequality 1:
$\frac{2x + 1}{7x - 1} > 5$
Move all terms to one side:
$\frac{2x + 1}{7x - 1} - 5 > 0$
Find a common denominator:
$\frac{2x + 1 - 5(7x - 1)}{7x - 1} > 0$
Simplify the numerator:
$\frac{2x + 1 - 35x + 5}{7x - 1} > 0$
$\frac{-33x + 6}{7x - 1} > 0$
Factor the numerator: $\frac{3(-11x + 2)}{7x - 1} > 0$. Since 3 is positive, the inequality is equivalent to:
$\frac{-11x + 2}{7x - 1} > 0$
The critical points are where the numerator or denominator is zero: $x = \frac{2}{11}$ and $x = \frac{1}{7}$. The expression is undefined at $x = \frac{1}{7}$.
We analyze the sign of $\frac{-11x + 2}{7x - 1}$ in the intervals $(-\infty, \frac{1}{7})$, $(\frac{1}{7}, \frac{2}{11})$, and $(\frac{2}{11}, \infty)$.
Testing points in each interval, we find that the expression is positive when $\frac{1}{7} < x < \frac{2}{11}$.
The solution for Inequality 1 is $\frac{1}{7} < x < \frac{2}{11}$. In interval notation: $(\frac{1}{7}, \frac{2}{11})$.
Solving Inequality 2:
$\frac{x + 7}{x - 8} > 2$
Move all terms to one side:
$\frac{x + 7}{x - 8} - 2 > 0$
Find a common denominator:
$\frac{x + 7 - 2(x - 8)}{x - 8} > 0$
Simplify the numerator:
$\frac{x + 7 - 2x + 16}{x - 8} > 0$
$\frac{-x + 23}{x - 8} > 0$
The critical points are where the numerator or denominator is zero: $x = 23$ and $x = 8$. The expression is undefined at $x = 8$.
We analyze the sign of $\frac{-x + 23}{x - 8}$ in the intervals $(-\infty, 8)$, $(8, 23)$, and $(23, \infty)$.
Testing points in each interval, we find that the expression is positive when $8 < x < 23$.
The solution for Inequality 2 is $8 < x < 23$. In interval notation: $(8, 23)$.
Finding the intersection:
The solution to the system of inequalities is the intersection of the solution sets of the individual inequalities.
Solution set for Inequality 1: $(\frac{1}{7}, \frac{2}{11})$
Solution set for Inequality 2: $(8, 23)$
We need to find the intersection of $(\frac{1}{7}, \frac{2}{11})$ and $(8, 23)$.
$\frac{1}{7} \approx 0.143$ and $\frac{2}{11} \approx 0.182$. So the first interval is approximately $(0.143, 0.182)$.
The second interval is $(8, 23)$.
Since the largest value in the first interval ($\frac{2}{11} \approx 0.182$) is less than the smallest value in the second interval (8), there is no overlap between the two intervals.
The intersection of $(\frac{1}{7}, \frac{2}{11})$ and $(8, 23)$ is the empty set.
Solution set:
The solution set for the given system of inequalities is the empty set, denoted by $\emptyset$ or \{\}.
Question 14. Find the linear inequalities for which the shaded region in the given figure is the solution set.

Answer:
Understanding the Problem:
The shaded region is the feasible region defined by a system of linear inequalities. The boundaries of the shaded region are formed by lines. We need to identify these lines and determine the corresponding inequalities.
Identifying Boundary Lines from the Figure:
Observing the given figure, the shaded region is bounded by four lines. Let's identify their equations:
1. The y-axis.
2. The x-axis.
3. A line passing through the points $(6, 0)$ on the x-axis and $(0, 3)$ on the y-axis.
4. A line passing through the points $(5, 0)$ on the x-axis and $(0, 5)$ on the y-axis.
All boundary lines appear to be solid, indicating that the inequalities are inclusive (with $\le$ or $\ge$).
Formulating Inequalities:
1. Boundary 1: The y-axis. The equation of the y-axis is $x = 0$. Since the shaded region is to the right of the y-axis, the inequality is $x \ge 0$.
2. Boundary 2: The x-axis. The equation of the x-axis is $y = 0$. Since the shaded region is above the x-axis, the inequality is $y \ge 0$.
3. Boundary 3: Line through $(6, 0)$ and $(0, 3)$. Using the intercept form $\frac{x}{a} + \frac{y}{b} = 1$, with $a=6$ and $b=3$, the equation is $\frac{x}{6} + \frac{y}{3} = 1$. Multiply by 6 to clear denominators: $6(\frac{x}{6}) + 6(\frac{y}{3}) = 6(1)$, which simplifies to $x + 2y = 6$. To find the inequality, test a point in the shaded region, e.g., the origin $(0, 0)$. Substitute $(0, 0)$ into $x + 2y$: $0 + 2(0) = 0$. Since the origin is in the shaded region and $0 \le 6$, the inequality is $x + 2y \le 6$.
4. Boundary 4: Line through $(5, 0)$ and $(0, 5)$. Using the intercept form $\frac{x}{a} + \frac{y}{b} = 1$, with $a=5$ and $b=5$, the equation is $\frac{x}{5} + \frac{y}{5} = 1$. Multiply by 5: $5(\frac{x}{5}) + 5(\frac{y}{5}) = 5(1)$, which simplifies to $x + y = 5$. To find the inequality, test the origin $(0, 0)$. Substitute $(0, 0)$ into $x + y$: $0 + 0 = 0$. Since the origin is in the shaded region and $0 \le 5$, the inequality is $x + y \le 5$.
System of Linear Inequalities:
Combining the inequalities for each boundary, the system of linear inequalities defining the shaded region is:
$x \ge 0$
$y \ge 0$
$x + 2y \le 6$
$x + y \le 5$
Question 15. Find the linear inequalities for which the shaded region in the given figure is the solution set.
Answer:
Understanding the Problem:
The shaded region is the feasible region of a system of linear inequalities. The boundaries of this region are formed by lines. We need to determine the equation for each boundary line and the direction of the inequality based on where the shaded region lies relative to the line.
Identifying Boundary Lines from the Figure:
Observing the given figure, the shaded region is bounded by three lines in the first quadrant. These lines are:
1. The y-axis.
2. The x-axis.
3. A slanted line passing through the points where it intersects the x-axis and the y-axis.
From the figure, the slanted line appears to pass through the point $(20, 0)$ on the x-axis and $(0, 30)$ on the y-axis. All boundary lines are solid, indicating inclusive inequalities ($\le$ or $\ge$).
Formulating Inequalities:
1. Boundary 1: The y-axis. The equation of the y-axis is $x = 0$. The shaded region is to the right of the y-axis. Since the line is solid, the inequality is $x \ge 0$.
2. Boundary 2: The x-axis. The equation of the x-axis is $y = 0$. The shaded region is above the x-axis. Since the line is solid, the inequality is $y \ge 0$.
3. Boundary 3: The line passing through $(20, 0)$ and $(0, 30)$. We can find the equation of this line using the intercept form $\frac{x}{a} + \frac{y}{b} = 1$, where $a$ is the x-intercept and $b$ is the y-intercept. Here, $a = 20$ and $b = 30$.
The equation of the line is $\frac{x}{20} + \frac{y}{30} = 1$.
To eliminate the denominators, multiply the entire equation by the least common multiple of 20 and 30, which is 60:
$60 \times \frac{x}{20} + 60 \times \frac{y}{30} = 60 \times 1$
$3x + 2y = 60$
Now, determine the inequality. The shaded region is below this line. We can test a point in the shaded region that is not on the line, such as the origin $(0, 0)$. Substitute the coordinates of the origin into the expression $3x + 2y$:
$3(0) + 2(0) = 0$
Compare this value to 60. Since the origin $(0, 0)$ is in the shaded region and $0 \le 60$, the inequality is $3x + 2y \le 60$. Since the line is solid, the inequality is inclusive.
System of Linear Inequalities:
Combining the inequalities derived from each boundary line, the system of linear inequalities that defines the shaded region is:
$x \ge 0$
$y \ge 0$
$3x + 2y \le 60$
Question 16. Show that the following system of linear inequalities has no solution
x + 2y ≤ 3, 3x + 4y ≥ 12, x ≥ 0, y ≥ 1
Answer:
Given System of Inequalities:
1) $x + 2y \le 3$
2) $3x + 4y \ge 12$
3) $x \ge 0$
4) $y \ge 1$
Analysis of the inequalities:
From inequality (1), we can express $x$ in terms of $y$: $x \le 3 - 2y$.
From inequality (2), we can express $x$ in terms of $y$: $3x \ge 12 - 4y \implies x \ge \frac{12 - 4y}{3} = 4 - \frac{4}{3}y$.
Inequality (3) gives a lower bound for $x$: $x \ge 0$.
Inequality (4) gives a lower bound for $y$: $y \ge 1$.
Combining the constraints:
For a solution $(x, y)$ to exist, it must satisfy all four inequalities simultaneously.
From inequalities (1) and (3), we have $0 \le x \le 3 - 2y$. For such an $x$ to exist, the upper bound must be greater than or equal to the lower bound:
$0 \le 3 - 2y$
$2y \le 3$
$y \le \frac{3}{2} = 1.5$
Combining this with inequality (4) ($y \ge 1$), any solution must satisfy $1 \le y \le 1.5$.
Now consider inequality (2) and the constraints on $x$. We need $x \ge 4 - \frac{4}{3}y$.
For a solution $(x, y)$ to exist that satisfies inequalities (1), (2), (3), and (4), we must have $x$ satisfying both $x \le 3 - 2y$ and $x \ge 4 - \frac{4}{3}y$, along with $x \ge 0$ and $y \ge 1$.
From $x \le 3 - 2y$ and $x \ge 4 - \frac{4}{3}y$, we must have:
$4 - \frac{4}{3}y \le 3 - 2y$
Add $2y$ to both sides and subtract 4 from both sides:
$2y - \frac{4}{3}y \le 3 - 4$
$\frac{6y - 4y}{3} \le -1$
$\frac{2}{3}y \le -1$
Multiply by $\frac{3}{2}$:
$y \le -\frac{3}{2} = -1.5$
Conclusion:
From inequalities (1), (3), and (4), we found that any solution must satisfy $1 \le y \le 1.5$.
However, by combining inequalities (1) and (2), we found that any solution must satisfy $y \le -1.5$.
The condition $1 \le y \le 1.5$ and the condition $y \le -1.5$ cannot both be true simultaneously for any real number $y$, because there is no number that is both greater than or equal to 1 and less than or equal to -1.5.
Since the constraints on $y$ derived from the system are contradictory, there is no pair of $(x, y)$ that can satisfy all inequalities in the system.
Therefore, the system of linear inequalities has no solution.
Question 17. Solve the following system of linear inequalities:
3x + 2y ≥ 24, 3x + y ≤ 15, x ≥ 4
Answer:
Given System of Inequalities:
1) $3x + 2y \ge 24$
2) $3x + y \le 15$
3) $x \ge 4$
Solving the inequalities:
We are looking for values of $x$ and $y$ that satisfy all three inequalities simultaneously. Let's analyze the constraints placed on $x$ and $y$ by each inequality.
From inequality (3), we have the constraint $x \ge 4$. This means any solution $(x, y)$ must have an x-coordinate greater than or equal to 4.
Now let's consider inequality (2): $3x + y \le 15$. We can isolate $y$:
$y \le 15 - 3x$
Since we know from inequality (3) that $x \ge 4$, we can find an upper bound for $y$ based on this minimum value of $x$. Substitute $x = 4$ into the expression for the upper bound of $y$:
$y \le 15 - 3(4)$
$y \le 15 - 12$
$y \le 3$
So, any solution satisfying inequalities (2) and (3) must have $x \ge 4$ and $y \le 3$.
Now let's consider inequality (1): $3x + 2y \ge 24$.
We need to check if there exist values of $x$ and $y$ such that $x \ge 4$, $y \le 3$, and $3x + 2y \ge 24$.
Let's evaluate the expression $3x + 2y$ under the constraints $x \ge 4$ and $y \le 3$.
Since $x \ge 4$, the minimum value of $3x$ is $3 \times 4 = 12$. Thus, $3x \ge 12$.
Since $y \le 3$, the maximum value of $2y$ is $2 \times 3 = 6$. Thus, $2y \le 6$.
Consider the sum $3x + 2y$. We know $3x \ge 12$. We also know $2y \le 6$. To satisfy $3x + 2y \ge 24$, we need the sum to be at least 24.
From $y \le 15 - 3x$ (from inequality 2) and $y \le 3$ (from inequality 3 combined with inequality 2), we need $15 - 3x$ and $3$ to give an upper bound for $y$. Specifically, $y \le \min(15 - 3x, 3)$.
Let's substitute the upper bound for $y$ from inequality (2) into inequality (1):
We have $y \le 15 - 3x$. Multiply by 2: $2y \le 2(15 - 3x) = 30 - 6x$.
Substitute this into $3x + 2y \ge 24$:
$3x + (2y) \ge 24$
$3x + (30 - 6x) \ge 24$ (This substitution is not quite right as $2y$ might be less than $30-6x$)
Let's use the constraint $x \ge 4$ and $y \le 3$ directly on $3x + 2y$.
From $x \ge 4$, multiply by 3: $3x \ge 12$.
From $y \le 3$, multiply by 2: $2y \le 6$.
Adding these two inequalities: $3x + 2y \ge 12 + (\text{some value} \le 6)$. This doesn't give a lower bound for $3x+2y$.
Let's use inequality (1) and (2) to get a constraint on $x$.
From (1), $2y \ge 24 - 3x$. So $y \ge 12 - \frac{3}{2}x$.
From (2), $y \le 15 - 3x$.
For a solution to exist, we must have $12 - \frac{3}{2}x \le y \le 15 - 3x$. This requires the lower bound to be less than or equal to the upper bound:
$12 - \frac{3}{2}x \le 15 - 3x$
Add $3x$ to both sides:
$12 - \frac{3}{2}x + 3x \le 15$
$12 + \frac{3}{2}x \le 15$
Subtract 12 from both sides:
$\frac{3}{2}x \le 3$
Multiply by $\frac{2}{3}$:
$x \le 3 \times \frac{2}{3}$
$x \le 2$
Conclusion:
From inequalities (1) and (2), any solution $(x, y)$ must satisfy $x \le 2$.
However, inequality (3) requires that any solution must satisfy $x \ge 4$.
The condition $x \le 2$ and the condition $x \ge 4$ are contradictory. There is no real number $x$ that is simultaneously less than or equal to 2 and greater than or equal to 4.
Since there is no value of $x$ that satisfies all the constraints on $x$ derived from the system of inequalities, there is no pair $(x, y)$ that can satisfy the entire system.
Therefore, the given system of linear inequalities has no solution.
Question 18. Show that the solution set of the following system of linear inequalities is an unbounded region
2x + y ≥ 8, x + 2y ≥ 10, x ≥ 0, y ≥ 0
Answer:
Given System of Inequalities:
1) $2x + y \ge 8$
2) $x + 2y \ge 10$
3) $x \ge 0$
4) $y \ge 0$
Graphical Approach:
To show that the solution set is an unbounded region, we can graph the boundary lines and determine the feasible region.
Consider the boundary line for inequality (1): $2x + y = 8$.
If $x = 0$, $y = 8$. Point $(0, 8)$.
If $y = 0$, $2x = 8 \implies x = 4$. Point $(4, 0)$.
Test the origin $(0, 0)$: $2(0) + 0 = 0$. $0 \ge 8$ is False. So the solution region for $2x + y \ge 8$ is on the side of the line $2x + y = 8$ that does not contain the origin.
Consider the boundary line for inequality (2): $x + 2y = 10$.
If $x = 0$, $2y = 10 \implies y = 5$. Point $(0, 5)$.
If $y = 0$, $x = 10$. Point $(10, 0)$.
Test the origin $(0, 0)$: $0 + 2(0) = 0$. $0 \ge 10$ is False. So the solution region for $x + 2y \ge 10$ is on the side of the line $x + 2y = 10$ that does not contain the origin.
Inequality (3): $x \ge 0$ represents the region to the right of or on the y-axis.
Inequality (4): $y \ge 0$ represents the region above or on the x-axis.
Inequalities (3) and (4) together restrict the solution to the first quadrant (including the positive x and y axes).
Determining the Feasible Region:
The feasible region is the set of points $(x, y)$ that satisfy all four inequalities. This is the intersection of the regions defined by each inequality.
We are looking for points in the first quadrant that are also above or on the line $2x + y = 8$ and above or on the line $x + 2y = 10$.
The vertices of the feasible region are the intersection points of the boundary lines within the first quadrant.
Intersection of $2x + y = 8$ and $x = 0$: $y = 8$. Point $(0, 8)$.
Intersection of $x + 2y = 10$ and $y = 0$: $x = 10$. Point $(10, 0)$.
Intersection of $2x + y = 8$ and $x + 2y = 10$:
From the first equation, $y = 8 - 2x$. Substitute into the second equation:
$x + 2(8 - 2x) = 10$
$x + 16 - 4x = 10$
$-3x = 10 - 16$
$-3x = -6$
$x = 2$
Substitute $x = 2$ back into $y = 8 - 2x$:
$y = 8 - 2(2) = 8 - 4 = 4$.
Intersection point: $(2, 4)$. This point is in the first quadrant, so it is a vertex.
The corner points of the feasible region are $(10, 0)$, $(2, 4)$, and $(0, 8)$.
The feasible region is the area that is above or on the line segment connecting $(10, 0)$ and $(2, 4)$, and above or on the line segment connecting $(2, 4)$ and $(0, 8)$, and is in the first quadrant.
Consider a point like $(10, 10)$. $2(10) + 10 = 30 \ge 8$ (True). $10 + 2(10) = 30 \ge 10$ (True). $10 \ge 0$ (True). $10 \ge 0$ (True). The point $(10, 10)$ is in the feasible region.
Consider points with very large $x$ and $y$ values, such that $x \ge 10$ and $y \ge 8$. For such points, $2x+y > 2(10)+8 = 28 \ge 8$ and $x+2y > 10+2(8) = 26 \ge 10$. Thus, the inequalities $2x+y \ge 8$ and $x+2y \ge 10$ are satisfied for all points $(x,y)$ in the region $x \ge 10, y \ge 8$. This region extends infinitely in the positive x and y directions.
More formally, the feasible region includes all points on and above the boundary lines $2x+y=8$ and $x+2y=10$ within the first quadrant. The region extends upwards and to the right indefinitely. For instance, the ray starting from $(10, 0)$ and extending horizontally to the right ($x \ge 10, y=0$) is part of the region boundary ($x+2y \ge 10$ and $y \ge 0$ are satisfied, and for $x \ge 10$, $2x+y = 2x \ge 20 \ge 8$). Similarly, the ray starting from $(0, 8)$ and extending vertically upwards ($x=0, y \ge 8$) is part of the region boundary ($2x+y \ge 8$ and $x \ge 0$ are satisfied, and for $y \ge 8$, $x+2y = 2y \ge 16 \ge 10$). The region above and to the right of the polygon formed by these lines and the axes extends infinitely.
Conclusion:
The feasible region is bounded by the lines $x=0$, $y=0$, $2x+y=8$, and $x+2y=10$. However, the region defined by $2x+y \ge 8$, $x+2y \ge 10$, $x \ge 0$, $y \ge 0$ is the area in the first quadrant that lies above or on both lines. This region extends infinitely in the positive x and positive y directions. Therefore, the solution set is an unbounded region.
Question 19 to 30 (Multiple Choice Questions)
Choose the correct answer from the given four options in each of the Exercises 19 to 26 (M.C.Q.).
Question 19. If x < 5, then
(A) – x < – 5
(B) – x ≤ – 5
(C) – x > – 5
(D) – x ≥ – 5
Answer:
Given inequality:
$x < 5$
Transformation:
We want to find the inequality involving $-x$. To get $-x$ from $x$, we multiply by $-1$.
When an inequality is multiplied or divided by a negative number, the direction of the inequality sign is reversed.
Multiply the inequality $x < 5$ by $-1$:
$(-1) \times x > (-1) \times 5$
$-x > -5$
Comparing with options:
The resulting inequality is $-x > -5$. Let's compare this with the given options:
(A) $-x < -5$
(B) $-x \le -5$
(C) $-x > -5$
(D) $-x \ge -5$
Our result matches option (C).
The correct option is (C).
Question 20. Given that x, y and b are real numbers and x < y, b < 0, then
(A) $\frac{x}{b}$ < $\frac{y}{b}$
(B) $\frac{x}{b}$ ≤ $\frac{y}{b}$
(C) $\frac{x}{b}$ > $\frac{y}{b}$
(D) $\frac{x}{b}$ ≥ $\frac{y}{b}$
Answer:
Given:
$x < y$
$b < 0$
$x, y, b$ are real numbers.
Operation:
We want to find the relationship between $\frac{x}{b}$ and $\frac{y}{b}$. This involves dividing the inequality $x < y$ by $b$.
When an inequality is multiplied or divided by a negative number, the direction of the inequality sign is reversed.
Since we are dividing by $b$, which is given to be negative ($b < 0$), the inequality sign must be reversed.
Starting with $x < y$, divide both sides by $b$:
$\frac{x}{b} > \frac{y}{b}$
Comparing with options:
The resulting inequality is $\frac{x}{b} > \frac{y}{b}$. Let's compare this with the given options:
(A) $\frac{x}{b} < \frac{y}{b}$
(B) $\frac{x}{b} \le \frac{y}{b}$
(C) $\frac{x}{b} > \frac{y}{b}$
(D) $\frac{x}{b} \ge \frac{y}{b}$
Our result matches option (C).
The correct option is (C).
Question 21. If – 3x + 17 < – 13, then
(A) x ∈ (10, ∞)
(B) x ∈ [10, ∞)
(C) x ∈ (– ∞, 10]
(D) x ∈ [– 10, 10)
Answer:
Given inequality:
$-3x + 17 < -13$
Solving the inequality:
Subtract 17 from both sides:
$-3x + 17 - 17 < -13 - 17$
$-3x < -30$
Divide both sides by -3. Remember to reverse the inequality sign when dividing by a negative number:
$\frac{-3x}{-3} > \frac{-30}{-3}$
$x > 10$
Expressing the solution in interval notation:
The inequality $x > 10$ means all real numbers strictly greater than 10.
In interval notation, this is written as $(10, \infty)$.
Comparing with options:
Let's compare our solution $(10, \infty)$ with the given options:
(A) x ∈ $(10, \infty)$
(B) x ∈ $[10, \infty)$
(C) x ∈ $(-\infty, 10]$
(D) x ∈ $[-10, 10)$
Our solution matches option (A).
The correct option is (A).
Question 22. If x is a real number and |x| < 3, then
(A) x ≥ 3
(B) – 3 < x < 3
(C) x ≤ – 3
(D) – 3 ≤ x ≤ 3
Answer:
Given inequality:
$|x| < 3$
Solving the inequality:
The inequality $|x| < k$, where $k$ is a positive constant, is equivalent to $-k < x < k$.
In this case, $k = 3$.
So, the inequality $|x| < 3$ is equivalent to:
$-3 < x < 3$
Comparing with options:
The resulting inequality is $-3 < x < 3$. Let's compare this with the given options:
(A) $x \ge 3$
(B) $-3 < x < 3$
(C) $x \le -3$
(D) $-3 \le x \le 3$
Our solution matches option (B).
The correct option is (B).
Question 23. x and b are real numbers. If b > 0 and |x| > b, then
(A) x ∈ (– b, ∞)
(B) x ∈ [– ∞, b)
(C) x ∈ (– b, b)
(D) x ∈ (– ∞, – b) ∪ (b, ∞)
Answer:
Given inequality:
$|x| > b$, where $b > 0$.
Solving the inequality:
The inequality $|x| > k$, where $k$ is a positive constant, is equivalent to $x < -k$ or $x > k$.
In this case, $k = b$.
So, the inequality $|x| > b$ is equivalent to:
$x < -b$ or $x > b$
Expressing the solution in interval notation:
The inequality $x < -b$ represents the interval $(-\infty, -b)$.
The inequality $x > b$ represents the interval $(b, \infty)$.
The solution set is the union of these two intervals:
$(-\infty, -b) \cup (b, \infty)$
Comparing with options:
Let's compare our solution with the given options:
(A) x ∈ $(-b, \infty)$
(B) x ∈ $[– \infty, b)$ (Note: $[-\infty, ...)$ is incorrect notation)
(C) x ∈ $(-b, b)$
(D) x ∈ $(-\infty, -b) \cup (b, \infty)$
Our solution matches option (D).
The correct option is (D).
Question 24. If |x - 1| > 5, then
(A) x ∈ (– 4, 6)
(B) x ∈ [– 4, 6]
(C) x ∈ [– ∞, – 4) ∪ (6, ∞)
(D) x ∈ [– ∞, – 4) ∪ [6, ∞)
Answer:
Given inequality:
$|x - 1| > 5$
Solving the inequality:
The inequality of the form $|A| > b$, where $b$ is a positive constant, is equivalent to $A < -b$ or $A > b$.
In this case, $A = x - 1$ and $b = 5$.
So, we have:
$x - 1 < -5$ or $x - 1 > 5$
Solve the first inequality:
$x - 1 < -5$
Add 1 to both sides:
$x - 1 + 1 < -5 + 1$
$x < -4$
Solve the second inequality:
$x - 1 > 5$
Add 1 to both sides:
$x - 1 + 1 > 5 + 1$
$x > 6$
Combining the solutions:
The solution to the original inequality is the union of the solutions from the two cases:
$x < -4$ or $x > 6$
In interval notation, $x < -4$ is represented as $(-\infty, -4)$.
In interval notation, $x > 6$ is represented as $(6, \infty)$.
The combined solution set is $(-\infty, -4) \cup (6, \infty)$.
Comparing with options:
Let's compare our solution with the given options:
(A) x ∈ $(-4, 6)$
(B) x ∈ $[-4, 6]$
(C) x ∈ $(– \infty, – 4) \cup (6, \infty)$ (Typo in option (C) should be (– ∞, – 4))
(D) x ∈ $[– \infty, – 4) \cup [6, \infty)$ (Note: $[-\infty, ...)$ and $[..., \infty)$ are incorrect notations when the endpoint is not included)
Assuming the typo in option (C), it matches our derived solution set.
The correct option is (C).
Question 25. If |x + 2| ≤ 9 , then
(A) x ∈ (– 7, 11)
(B) x ∈ [– 11, 7]
(C) x ∈ (– ∞, – 7) ∪ (11, ∞)
(D) x ∈ (– ∞, – 7) ∪ [11, ∞)
Answer:
Given inequality:
$|x + 2| \le 9$
Solving the inequality:
The inequality of the form $|A| \le b$, where $b$ is a positive constant, is equivalent to $-b \le A \le b$.
In this case, $A = x + 2$ and $b = 9$.
So, we have:
$-9 \le x + 2 \le 9$
To isolate $x$, subtract 2 from all parts of the inequality:
$-9 - 2 \le x + 2 - 2 \le 9 - 2$
$-11 \le x \le 7$
Expressing the solution in interval notation:
The inequality $-11 \le x \le 7$ means all real numbers between -11 and 7, including both endpoints.
In interval notation, this is written as $[-11, 7]$.
Comparing with options:
Let's compare our solution $[-11, 7]$ with the given options:
(A) x ∈ $(-7, 11)$
(B) x ∈ $[-11, 7]$
(C) x ∈ $(-\infty, -7) \cup (11, \infty)$
(D) x ∈ $(-\infty, -7) \cup [11, \infty)$
Our solution matches option (B).
The correct option is (B).
Question 26. The inequality representing the following graph is:

(A) |x| < 5
(B) |x| ≤ 5
(C) |x| > 5
(D) |x| ≥ 5
Answer:
Interpretation of the graph:
The graph shows a number line with shaded regions. The shaded regions are to the left of -5 and to the right of 5.
There are open circles (or parenthetical endpoints) at -5 and 5, indicating that these points are not included in the solution set.
The region to the left of -5 represents $x < -5$.
The region to the right of 5 represents $x > 5$.
The solution set represented by the graph is the union of these two regions: $x < -5$ or $x > 5$.
In interval notation, this is $(-\infty, -5) \cup (5, \infty)$.
Relating to absolute value inequalities:
We need to find which absolute value inequality corresponds to the solution set $x < -5$ or $x > 5$.
Recall the standard forms of absolute value inequalities:
- $|x| < k$ corresponds to $-k < x < k$.
- $|x| \le k$ corresponds to $-k \le x \le k$.
- $|x| > k$ corresponds to $x < -k$ or $x > k$.
- $|x| \ge k$ corresponds to $x \le -k$ or $x \ge k$.
Comparing our solution $x < -5$ or $x > 5$ with these forms, we see that it matches the form $x < -k$ or $x > k$ with $k = 5$.
Therefore, the inequality representing the graph is $|x| > 5$.
Comparing with options:
Let's compare our derived inequality $|x| > 5$ with the given options:
(A) $|x| < 5$ (Solution: $-5 < x < 5$)
(B) $|x| \le 5$ (Solution: $-5 \le x \le 5$)
(C) $|x| > 5$ (Solution: $x < -5$ or $x > 5$)
(D) $|x| \ge 5$ (Solution: $x \le -5$ or $x \ge 5$)
Our derived inequality matches option (C).
The correct option is (C).
Solution of a linear inequality in variable x is represented on number line in Exercises 27 to 30. Choose the correct answer from the given four options in each of the exercises (M.C.Q.).
Question 27.

(A) x ∈ (– ∞, 5)
(B) x ∈ (– ∞, 5]
(C) x ∈ [5, ∞)
(D) x ∈ (5, ∞)
Answer:
Interpretation of the graph:
The graph shows a number line with a shaded region starting at the point 5 and extending indefinitely to the right.
The point at 5 is marked with a solid circle, indicating that the number 5 is included in the solution set.
Corresponding inequality and interval notation:
The shaded region represents all real numbers that are greater than or equal to 5.
In inequality form, this is written as $x \ge 5$.
In interval notation, this is written as $[5, \infty)$.
Comparing with options:
Let's compare our derived solution $[5, \infty)$ with the given options:
(A) x ∈ $(– ∞, 5)$ represents $x < 5$.
(B) x ∈ $(– ∞, 5]$ represents $x \le 5$.
(C) x ∈ $[5, ∞)$ represents $x \ge 5$.
(D) x ∈ $(5, ∞)$ represents $x > 5$.
Our derived solution matches option (C).
The correct option is (C).
Question 28.

(A) x ∈ ($\frac{9}{2}$ , ∞)
(B) x ∈ [$\frac{9}{2}$ , ∞)
(C) x ∈ [- ∞ , $\frac{9}{2}$)
(D) x ∈ (- ∞ , $\frac{9}{2}$]
Answer:
Interpretation of the graph:
The graph shows a number line with a shaded region. The shaded region starts to the left of the point $\frac{9}{2}$ and extends indefinitely to the left.
The point at $\frac{9}{2}$ is marked with an open circle, indicating that the number $\frac{9}{2}$ is not included in the solution set.
Corresponding inequality and interval notation:
The shaded region represents all real numbers that are strictly less than $\frac{9}{2}$.
In inequality form, this is written as $x < \frac{9}{2}$.
In interval notation, this is written as $(-\infty, \frac{9}{2})$.
Comparing with options:
Let's compare our derived solution $(-\infty, \frac{9}{2})$ with the given options:
(A) x ∈ $(\frac{9}{2}, \infty)$ represents $x > \frac{9}{2}$.
(B) x ∈ $[\frac{9}{2}, \infty)$ represents $x \ge \frac{9}{2}$.
(C) x ∈ $(-\infty, \frac{9}{2})$ represents $x < \frac{9}{2}$.
(D) x ∈ $(-\infty, \frac{9}{2}]$ represents $x \le \frac{9}{2}$.
Our derived solution matches option (C).
The correct option is (C).
Question 29.
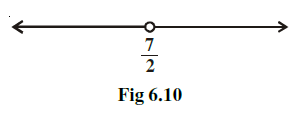
(A) x ∈ (- ∞ , $\frac{7}{2}$)
(B) x ∈ (- ∞ , $\frac{7}{2}$]
(C) x ∈ [$\frac{7}{2}$ , ∞)
(D) x ∈ ($\frac{7}{2}$ , ∞)
Answer:
Interpretation of the graph:
The graph shows a number line with a shaded region. The shaded region starts at the point $\frac{7}{2}$ and extends indefinitely to the right.
The point at $\frac{7}{2}$ is marked with a solid circle, indicating that the number $\frac{7}{2}$ is included in the solution set.
Corresponding inequality and interval notation:
The shaded region represents all real numbers that are greater than or equal to $\frac{7}{2}$.
In inequality form, this is written as $x \ge \frac{7}{2}$.
In interval notation, this is written as $[\frac{7}{2}, \infty)$.
Comparing with options:
Let's compare our derived solution $[\frac{7}{2}, \infty)$ with the given options:
(A) x ∈ $(-\infty, \frac{7}{2})$ represents $x < \frac{7}{2}$.
(B) x ∈ $(-\infty, \frac{7}{2}]$ represents $x \le \frac{7}{2}$.
(C) x ∈ $[\frac{7}{2}, \infty)$ represents $x \ge \frac{7}{2}$.
(D) x ∈ $(\frac{7}{2}, \infty)$ represents $x > \frac{7}{2}$.
Our derived solution matches option (C).
The correct option is (C).
Question 30.

(A) x ∈ (- ∞ , - 2)
(B) x ∈ (- ∞, - 2]
(C) x ∈ (- 2, ∞]
(D) x ∈[- 2, ∞)
Answer:
Interpretation of the graph:
The graph shows a number line with a shaded region. The shaded region starts at the point -2 and extends indefinitely to the right.
The point at -2 is marked with a solid circle, indicating that the number -2 is included in the solution set.
Corresponding inequality and interval notation:
The shaded region represents all real numbers that are greater than or equal to -2.
In inequality form, this is written as $x \ge -2$.
In interval notation, this is written as $[-2, \infty)$.
Comparing with options:
Let's compare our derived solution $[-2, \infty)$ with the given options:
(A) x ∈ $(-\infty, -2)$ represents $x < -2$.
(B) x ∈ $(-\infty, -2]$ represents $x \le -2$.
(C) x ∈ $(-2, \infty]$ represents $x > -2$. (Note: $(..., \infty]$ is incorrect notation)
(D) x ∈ $[-2, \infty)$ represents $x \ge -2$.
Our derived solution matches option (D).
The correct option is (D).
Question 31 (True or False)
Question 31. State which of the following statements is True or False
(i) If x < y and b < 0, then $\frac{x}{b}$ < $\frac{y}{b}$
(ii) If xy > 0, then x > 0 and y < 0
(iii) If xy > 0, then x < 0 and y < 0
(iv) If xy < 0, then x < 0 and y < 0
(v) If x < –5 and x < –2, then x ∈ (– ∞, – 5)
(vi) If x < –5 and x > 2, then x ∈ (– 5, 2)
(vii) If x > –2 and x < 9, then x ∈ (– 2, 9)
(viii) If |x| > 5, then x ∈ (– ∞, – 5) ∪ [5, ∞)
(ix) If |x| ≤ 4, then x ∈ [– 4, 4]
(x) Graph of x < 3 is

(xi) Graph of x ≥ 0 is

(xii) Graph of y ≤ 0 is
(xiii) Solution set of x ≥ 0 and y ≤ 0 is

(xiv) Solution set of x ≥ 0 and y ≤ 1 is

(xv) Solution set of x + y ≥ 0 is

Answer:
Let's evaluate each statement:
(i) If $x < y$ and $b < 0$, then $\frac{x}{b} < \frac{y}{b}$
When dividing an inequality by a negative number, the inequality sign is reversed. So, if $x < y$ and $b < 0$, then $\frac{x}{b} > \frac{y}{b}$.
False
(ii) If $xy > 0$, then $x > 0$ and $y < 0$
If the product of two numbers is positive, they must have the same sign (both positive or both negative). The statement claims they have opposite signs (positive and negative), which results in a negative product.
False
(iii) If $xy > 0$, then $x < 0$ and $y < 0$
If the product of two numbers is positive ($xy > 0$), it means either ($x > 0$ and $y > 0$) or ($x < 0$ and $y < 0$). The statement claims it is *always* the latter, which is not true.
False
(iv) If $xy < 0$, then $x < 0$ and $y < 0$
If the product of two numbers is negative, they must have opposite signs. The statement claims they are both negative, which results in a positive product.
False
(v) If $x < –5$ and $x < –2$, then $x \in (– ∞, – 5)$
We need to satisfy both conditions: $x < -5$ and $x < -2$. Any number less than -5 is also less than -2. The intersection of the solution sets is the set of numbers less than -5, which is $(-\infty, -5)$.
True
(vi) If $x < –5$ and $x > 2$, then $x \in (– 5, 2)$
We need to satisfy both conditions: $x < -5$ and $x > 2$. There is no real number that is both less than -5 and greater than 2. The intersection of the solution sets is the empty set, $\emptyset$. The interval $(-5, 2)$ represents $-5 < x < 2$.
False
(vii) If $x > –2$ and $x < 9$, then $x \in (– 2, 9)$
We need to satisfy both conditions: $x > -2$ and $x < 9$. The numbers that satisfy both are those strictly between -2 and 9, i.e., $-2 < x < 9$. The interval notation for this is $(-2, 9)$.
True
(viii) If $|x| > 5$, then $x \in (– ∞, – 5) \cup [5, ∞)$
The inequality $|x| > 5$ means $x < -5$ or $x > 5$. In interval notation, this is $(-\infty, -5) \cup (5, \infty)$. The statement includes the endpoint 5 in the second interval, which corresponds to $\ge$ rather than $>$.
False
(ix) If $|x| \le 4$, then $x \in [– 4, 4]$
The inequality $|x| \le 4$ is equivalent to $-4 \le x \le 4$. In interval notation, this is $[-4, 4]$.
True
(x) Graph of $x < 3$ is ... (Image 11)
The graph for $x < 3$ should show an open circle at 3 and shading to the left. Assuming Image 11 correctly depicts this.
True (Assuming the image matches the standard graph of $x < 3$)
(xi) Graph of $x \ge 0$ is ... (Image 12)
The graph for $x \ge 0$ should show a closed circle at 0 and shading to the right. Assuming Image 12 correctly depicts this.
True (Assuming the image matches the standard graph of $x \ge 0$)
(xii) Graph of $y \le 0$ is ... (Image 13)
The graph for $y \le 0$ in a 2D plane should show the region below or on the x-axis (solid x-axis, region below shaded). Assuming Image 13 correctly depicts this.
True (Assuming the image matches the standard graph of $y \le 0$)
(xiii) Solution set of $x \ge 0$ and $y \le 0$ is ... (Image 14)
This system represents the intersection of the region $x \ge 0$ (right of/on y-axis) and $y \le 0$ (below/on x-axis). The intersection is the fourth quadrant, including the positive x-axis and the negative y-axis. Assuming Image 14 correctly depicts this region.
True (Assuming the image matches the standard graph of $x \ge 0$ and $y \le 0$)
(xiv) Solution set of $x \ge 0$ and $y \le 1$ is ... (Image 15)
This system represents the intersection of the region $x \ge 0$ (right of/on y-axis) and $y \le 1$ (below/on horizontal line $y=1$). This is the region in the first and fourth quadrants below or on the line $y=1$. Assuming Image 15 correctly depicts this region.
True (Assuming the image matches the standard graph of $x \ge 0$ and $y \le 1$)
(xv) Solution set of $x + y \ge 0$ is ... (Image 16)
The inequality $x + y \ge 0$ is equivalent to $y \ge -x$. The boundary line is $y = -x$, which is solid. The region is above or on this line (test point (1,0): $1+0 = 1 \ge 0$ is true). Assuming Image 16 correctly depicts the solid line $y=-x$ with the region above it shaded.
True (Assuming the image matches the standard graph of $x + y \ge 0$)
Question 32 (Fill in the Blanks)
Question 32. Fill in the blanks of the following:
(i) If – 4x ≥ 12, then x ... – 3.
(ii) If $\frac{-3}{4}$ x ≤ - 3, then x … 4.
(iii) If $\frac{2}{x + 2}$ > 0, then x … -2.
(iv) If x > – 5, then 4x ... –20.
(v) If x > y and z < 0, then – xz ... – yz.
(vi) If p > 0 and q < 0, then p – q ... p.
(vii) If |x + 2| > 5, then x ... - 7 or x … 3.
(viii) If - 2x + 1 ≥ 9, then x ... -4.
Answer:
Let's fill in the blanks by solving or analyzing each inequality/statement:
(i) If – 4x ≥ 12, then x $\ldots$ – 3.
Given $-4x \ge 12$. Divide by -4 and reverse the inequality sign: $\frac{-4x}{-4} \le \frac{12}{-4}$, which gives $x \le -3$.
Fill in the blank with $\le$.
(ii) If $\frac{-3}{4}$ x ≤ - 3, then x $\ldots$ 4.
Given $\frac{-3}{4}x \le -3$. Multiply by $-\frac{4}{3}$ and reverse the inequality sign: $(-\frac{4}{3}) \times (\frac{-3}{4}x) \ge (-\frac{4}{3}) \times (-3)$, which gives $x \ge 4$.
Fill in the blank with $\ge$.
(iii) If $\frac{2}{x + 2}$ > 0, then x $\ldots$ -2.
For the fraction $\frac{2}{x + 2}$ to be positive, the numerator (2, which is positive) and the denominator ($x + 2$) must have the same sign. So, $x + 2$ must be positive: $x + 2 > 0$, which gives $x > -2$.
Fill in the blank with $>$.
(iv) If x > – 5, then 4x $\ldots$ –20.
Given $x > -5$. Multiply by 4 (a positive number): $4 \times x > 4 \times (-5)$, which gives $4x > -20$.
Fill in the blank with $>$.
(v) If x > y and z < 0, then – xz $\ldots$ – yz.
Given $x > y$ and $z < 0$. Multiply $x > y$ by $z$. Since $z$ is negative, reverse the sign: $xz < yz$. Now, multiply $xz < yz$ by -1. Since -1 is negative, reverse the sign again: $-xz > -yz$.
Fill in the blank with $>$.
(vi) If p > 0 and q < 0, then p – q $\ldots$ p.
Consider the difference $(p - q) - p = -q$. Since $q < 0$, $-q$ is positive (e.g., if $q = -2$, then $-q = 2$). So, $-q > 0$. This means $(p - q) - p > 0$, which implies $p - q > p$.
Fill in the blank with $>$.
(vii) If |x + 2| > 5, then x $\ldots$ - 7 or x $\ldots$ 3.
The inequality $|A| > b$ is equivalent to $A < -b$ or $A > b$. Here $A = x + 2$ and $b = 5$. So, $x + 2 < -5$ or $x + 2 > 5$. Solving the first part: $x < -5 - 2 \implies x < -7$. Solving the second part: $x > 5 - 2 \implies x > 3$. The solution is $x < -7$ or $x > 3$.
Fill in the blanks with $<$ and $>$.
(viii) If - 2x + 1 ≥ 9, then x $\ldots$ -4.
Given $-2x + 1 \ge 9$. Subtract 1 from both sides: $-2x \ge 9 - 1 \implies -2x \ge 8$. Divide by -2 and reverse the sign: $\frac{-2x}{-2} \le \frac{8}{-2}$, which gives $x \le -4$.
Fill in the blank with $\le$.

